This is a draft written by Cameron Domenico Kirk-Giannini, assistant professor at Rutgers University, and Simon Goldstein, associate professor at the Dianoia Institute of Philosophy at ACU, as part of a series of papers for the Center for AI Safety Philosophy Fellowship's midpoint. Dan helped post to the Alignment Forum. This draft is meant to solicit feedback. The authors would especially welcome pointers to work related to the topic which they have not cited.
Abstract:
If it is possible to construct artificial superintelligences, it is likely that they will be extremely powerful. A natural question is how many such superintelligences to expect. Will the future be shaped by a single superintelligence (a unipolar outcome), or will there be multiple superintelligences shaping the future through their cooperative or adversarial interactions (a multipolar outcome)? We refer to this question as the polarity problem. This paper investigates the polarity problem. First, we consider the question of safety, suggesting that multipolar outcomes are likely to be safer for humanity than unipolar outcomes because humans are less likely to be disempowered in multipolar scenarios. Then we develop a series of causal models of AI agents that make predictions about the relative likelihood of unipolar as opposed to multipolar outcomes. Central to our models are three parameters: the time it takes for an AI attacker to develop an attack against an AI defender, the time it takes for the AI defender to develop its defense, and how far the defender lags behind the attacker temporally. We use our models to identify possible interventions which could change the probability of a multipolar outcome, thereby leading to a safer trajectory for AI development.
1. The Question
If it is possible to construct artificial superintelligences, it is likely that they will be extremely capable actors. Indeed, artificial superintelligences will likely be so much more capable than traditional actors that if they come into existence and function autonomously to gain and maintain power, the future will be shaped more or less exclusively by them.
If the future may be shaped more or less exclusively by artificial superintelligences, a natural question is how many such superintelligences to expect. Will the future be shaped by a single extremely powerful artificial superintelligence, or will there be multiple artificial superintelligences shaping the future through their cooperative or adversarial interactions? Call the former kind of outcome a unipolar scenario and the latter kind of outcome a multipolar scenario. And call the problem of calculating the probability of a unipolar scenario conditional on the existence of at least one strategic, power-seeking artificial general intelligence the polarity problem.
A natural first thought about the polarity problem is that if a strategic, power-seeking artificial general intelligence accrues enough power to exert substantial control over the future, we should expect it to use this power to prevent other AI systems from accruing a similar level of power. If other systems are insufficiently established at this point to defend themselves, the likely outcome will be a unipolar scenario. Thus one might expect that if the first strategic, power-seeking artificial general intelligence accrues power quickly compared to the lag between its rise and the rise of the second such system, the result will be a unipolar scenario.
Yet this natural first thought leaves much to be desired in terms of clarity and specificity. Exactly how many parameters are relevant in determining whether a given scenario results in a unipolar or multipolar outcome, and how exactly do the probabilities we assign to different values of these parameters determine the probability of a unipolar outcome?
We begin by answering the Why care? question. We suggest that polarity has implications for the safety of humanity because multipolar outcomes are likely to be safer than unipolar outcomes.
After reflecting on the safety implications of polarity, we develop a series of models which answer these questions, evaluate what they can tell us about the comparative probabilities of unipolar and multipolar scenarios, and consider their practical upshots for AI safety research.
2. Polarity and Safety
The bulk of this paper explores whether unipolar or multipolar scenarios are more likely. But before we consider this question, it is worth asking which kind of scenario would be better for humanity. We suggest that multipolar scenarios tend to be safer than unipolar scenarios. This discussion will help orient the rest of the paper, since it will allow us to evaluate how each intervention that influences polarity would contribute to AI safety.
In what follows, we use the term ‘AGI’ to mean any strategic, power-seeking artificial general intelligence. We assume that any AGI has strategic awareness and is capable of agentic planning, in the sense of Carlsmith (2021).[1] We also assume that any AGI possesses a capacity for recursive self-improvement and, if able, will exercise this capacity to enhance its capabilities.[2] This is why, although our definition of the polarity problem makes reference to AGIs which might or might not be superintelligent and the models we develop in what follows do not assume that the relevant AGI actors are superintelligent, we take it for granted that the surviving AGI actors in either unipolar or multipolar scenarios will eventually attain superintelligence.
To begin thinking about the safety implications of unipolarity and multipolarity, consider the following thought experiment. Imagine that the base rate of aligned AGIs is ten percent. That is, each time a new AGI comes into existence, there is a ten percent chance that its values will be aligned with those of humanity. Now consider which outcome is safer for humanity: First, you could have a unipolar outcome in which a single AGI superintelligence defeats all others. Second, you could have a multipolar outcome with a large population of AGI superintelligences coordinating and competing with one another. As the size of the multipolar population increases, the law of large numbers pushes this choice towards: either a single AGI superintelligence with a ten percent chance of alignment, or a large population of AGI superintelligences, ten percent of which are aligned.
We think the multipolar outcome will likely be better for humanity. In that outcome, ten percent of the AGI superintelligences will be our aligned advocates. Humanity has a better chance of surviving in this outcome than it does in the scenarios where there is only a ten percent chance that the single AGI superintelligence is aligned.
Generalizing from this thought experiment, the probability that a unipolar outcome is safe is roughly the probability that an AGI superintelligence will be aligned. By contrast, multipolar outcomes are more complex. First, humanity may survive a multipolar outcome even when the probability of AGI alignment isn’t very high, as long as a critical mass of AGI superintelligences are aligned. Second, even when most of the superintelligent AGIs in a multipolar scenario are not aligned, humanity may still wield influence as part of a strategic coalition. In international relations, smaller states are often able to exert influence as a part of multilateral coalitions.
On the other hand, multipolar outcomes also present unique risks to humans compared to unipolar outcomes. Even when many AGI superintelligences are aligned, humanity may be threatened when multipolar outcomes lead to negative sum behavior, such as long-term ineffectual warfare. In that case, humanity may end up as a ‘civilian casualty’ of AI conflict. As the probability of persistent conflict decreases, multipolar outcomes become safer for humanity than unipolar outcomes. In multipolar outcomes, humanity is less likely to become disempowered. And when persistent conflict is rare, humanity also avoids the risk of becoming collateral damage.
We acknowledge that there are important questions to be asked here about the probability of persistent conflict and other threats to human existence and wellbeing conditional on a multipolar outcome, and that certain answers to this question might entail that it is actually safer for humanity to take a one-time risk of extinction by rolling the dice on whether the single AGI in a unipolar scenario is aligned.[3] But our sense is that it is on balance prudentially rational for humanity to prefer a multipolar scenario to a unipolar one.
Summing up, our tentative judgment is that multipolar outcomes are safer in expectation than unipolar outcomes. Multipolarity opens up additional opportunities for safety, besides the chance of a single aligned AGI superintelligence.
Throughout the paper, we make a series of safety recommendations, all in the direction of multipolarity. If you think that unipolarity is safer than multipolarity, then you can just reverse the direction of each of our safety recommendations. On the other hand, if you think that polarity is not relevant to safety, then our safety recommendations below may not have very much relevance. Still, one factor that you may consider relevant even then is how likely persistent conflict is to emerge. While this is not the focus of our discussion below, many of the dynamics explored in our models also have bearing on this question.
Note that the models we develop below abstract away from two possible ways for humans to intervene on the course of events to improve safety. First, humans could simply resolve never to develop strategic, power-seeking artificial general intelligences. The feasibility of this intervention depends on a number of factors including the strength of the economic and military incentives to create autonomous AI systems with strategic awareness and the soundness of “instrumental convergence” reasoning, which suggests that most AGIs will be power-seeking. Second, humans could institute effective systems for detecting and disabling AGIs which might disempower them. To the best of our knowledge, the feasibility of this intervention is an open question; it would require the discovery of effective approaches to scalable oversight and/or the shutdown problem. The polarity-affecting interventions we explore below should be understood in the context of these other possible interventions.
Now that we’ve clarified the relevance of polarity to AI safety, we turn to the polarity problem.
3. The Lag-Attack-Defense Model
In this section, we introduce a simple model of the polarity problem — the Lag-Attack-Defense (LAD) Model — on which our subsequent discussion will be based.
The LAD model formalizes the following rough sketch of the polarity problem. It would be instrumentally valuable to a suitably powerful AGI to preclude the existence of other agents powerful enough to stop it from realizing its plans. Imagine that the first such AGI is aware that it is the first such AGI. Then the first suitably powerful AGI will be motivated to plan and execute an attack on all other potentially superintelligent actors as soon as it is able.
In light of the fact that it would be instrumentally valuable to a suitably powerful AGI to plan and execute an attack on all other potentially superintelligent actors, we should expect any later AGI to plan a defense against potential attacks. The solution to the polarity problem therefore depends on whether, when the first suitably powerful AGI executes its attack, any other potentially superintelligent actors have already executed a defense. This, in turn, depends on how far the second AGI’s developmental trajectory lags behind the first’s, how long it takes to plan and execute an attack, and how long it takes to plan and execute a defense (hence Lag-Attack-Defense).
To make this intuitive picture more precise, let us introduce a few definitions. Say that an AGI is released if it is autonomously pursuing its goals. An AGI might be released intentionally by its designers, or it might be released accidentally or through its own efforts.
Define takeoff as the process which begins when an AGI comes into existence and ends when it (i) is released and (ii) attains the capacity to plan and execute an attack or defense. As we are using the term, takeoff could end before an AGI becomes superintelligent. But if an AGI which is not superintelligent survives takeoff and is not later disabled, it is likely eventually to become superintelligent through recursive self-improvement.
Takeoff might look different for different AGI agents. For example, some might become superintelligent before being released, while others might be released before they become superintelligent. Nevertheless, the model will assume that the takeoff process takes the same amount of time for different AGI agents. See Section 13 for discussion of the effects of relaxing this requirement.
Finally, let an attack be any action taken by an AGI which results in the permanent disempowerment of some other actor if that actor has not mounted a defense.
The simple LAD model has four parameters, each representing an amount of time:
- Takeoff Time (TT): The duration of the takeoff process.
- Lag Time (LT): The time between the beginning of the first AGI’s takeoff and the beginning of the second AGI’s takeoff.
- Attack Time (AT): The time it takes for a post-takeoff AGI to plan and execute an attack.
- Defense Time (DT): The time it takes for a post-takeoff AGI to plan and execute a defense.
Note that the simple LAD model’s four parameters implicitly encode information about the finer-grained causal structure of any given case. For example, if the first AGIs to complete takeoff will not initially have access to the Internet, then attack and defense times will be longer. On the other hand, if the first AGIs will be very advanced when they complete takeoff (for example because they attain superintelligence before being released), attack and defense times will be shorter. Along similar lines, Bostrom’s (2014, 79) discussion of the idea of a “headwind” facing the frontrunner in the race to develop AGIs can be thought of as an argument about the value of LT. In this way, we pick time as our choice of unit, and then convert other variables like computational power, material resources, and intelligence into time through their effect on AT, DT, and LT.
The simple LAD model makes a number of assumptions:
- It assumes that the first AGI to complete takeoff must either attack or pursue other goals, and that the AGI lagging behind the first must either defend or pursue other goals (that is, it assumes fixed roles). Given this assumption, we will sometimes refer to the first AGI as the attacker and the second as the defender.
- It assumes that the attacker will plan and execute an attack as soon as it possible and that the defender will plan and execute a defense as soon as possible, unless it is precluded from doing so by a successful attack (that is, it assumes automatic behavior).
- It assumes that these AGIs have full information about which starts takeoff first and which starts takeoff second (that is, it assumes positional awareness).
- It assumes that there are only two AGIs (that is, it is a two-agent model).
- It assumes that an attack is successful if and only if it is carried out against a system which has not completed a defense (that is, it assumes deterministic outcomes).[4]
- It assumes that there is only one round of actions (that is, it assumes a one-shot structure to the interactions between AGI agents).
- It assumes that each AGI chooses how to act without information about how other AGIs have chosen to act (that is, it assumes private deliberation).
- It assumes that conflict between AGI agents cannot be avoided through bargaining (that is, it assumes the rationality of conflict).[5]
In later sections, we will relax the first four assumptions. In this paper, we don’t explore the consequences of giving up assumptions 5-8 at length. See Section 13, however, for discussion of further research directions arising from lifting these assumptions.
Let t0 be the moment which marks the beginning of the first AGI’s takeoff, t1 be the moment which marks the beginning of the second AGI’s takeoff, and t2 be the moment at which the first attack or defense is executed, whichever comes first.
The simple LAD model predicts that the amount of time which must elapse between t0 and the earliest possible attack is TT + AT, and that the amount of time which must elapse between t0 the earliest possible defense is LT + TT + DT. Therefore, a unipolar outcome occurs just in case time t0 + TT + AT precedes time t0 + TT + LT + DT, or equivalently the duration TT + AT is shorter than the duration TT + LT +DT. Since TT appears in both terms in this inequality, we can ignore it and simply consider whether AT is shorter than LT + DT. This is one of the upshots of the simple LAD model: takeoff time is not causally relevant to polarity.[6]
In an important sense, the simple LAD model encodes a bias towards offense over defense. Consider the equation AT < LT + DT. It is not enough for the defender to be able to prepare defenses as quickly as the attacker prepares attacks. Rather, the defender must work harder in order to offset its lag time.
To visualize these dynamics, compare the two diagrams below. In the first diagram, the attacker (A) attacks before the defender (D) is able to defend, resulting in a unipolar outcome. In the second diagram, D is able to plan and execute a defense before A finishes planning its attack, resulting in a multipolar outcome.
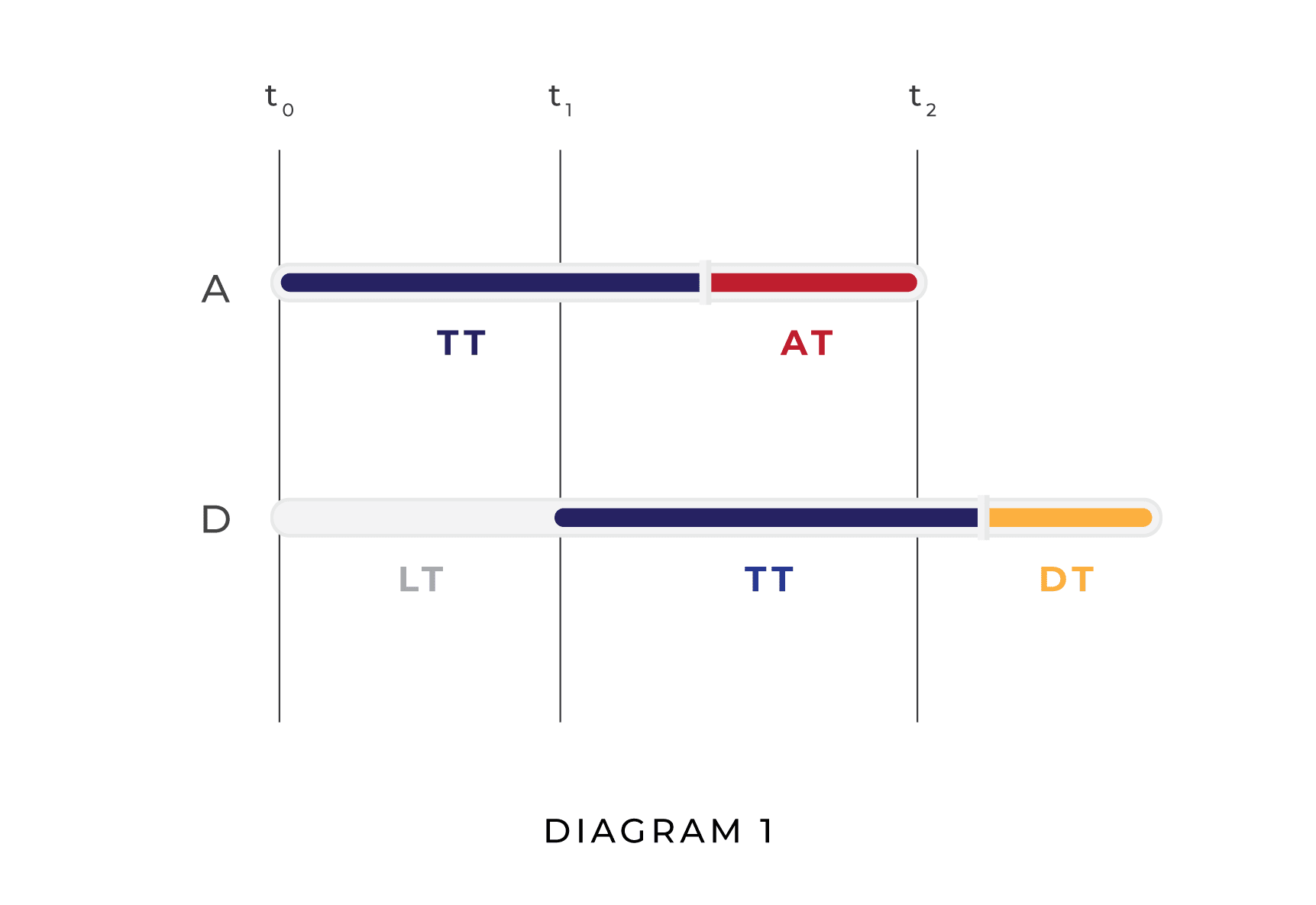
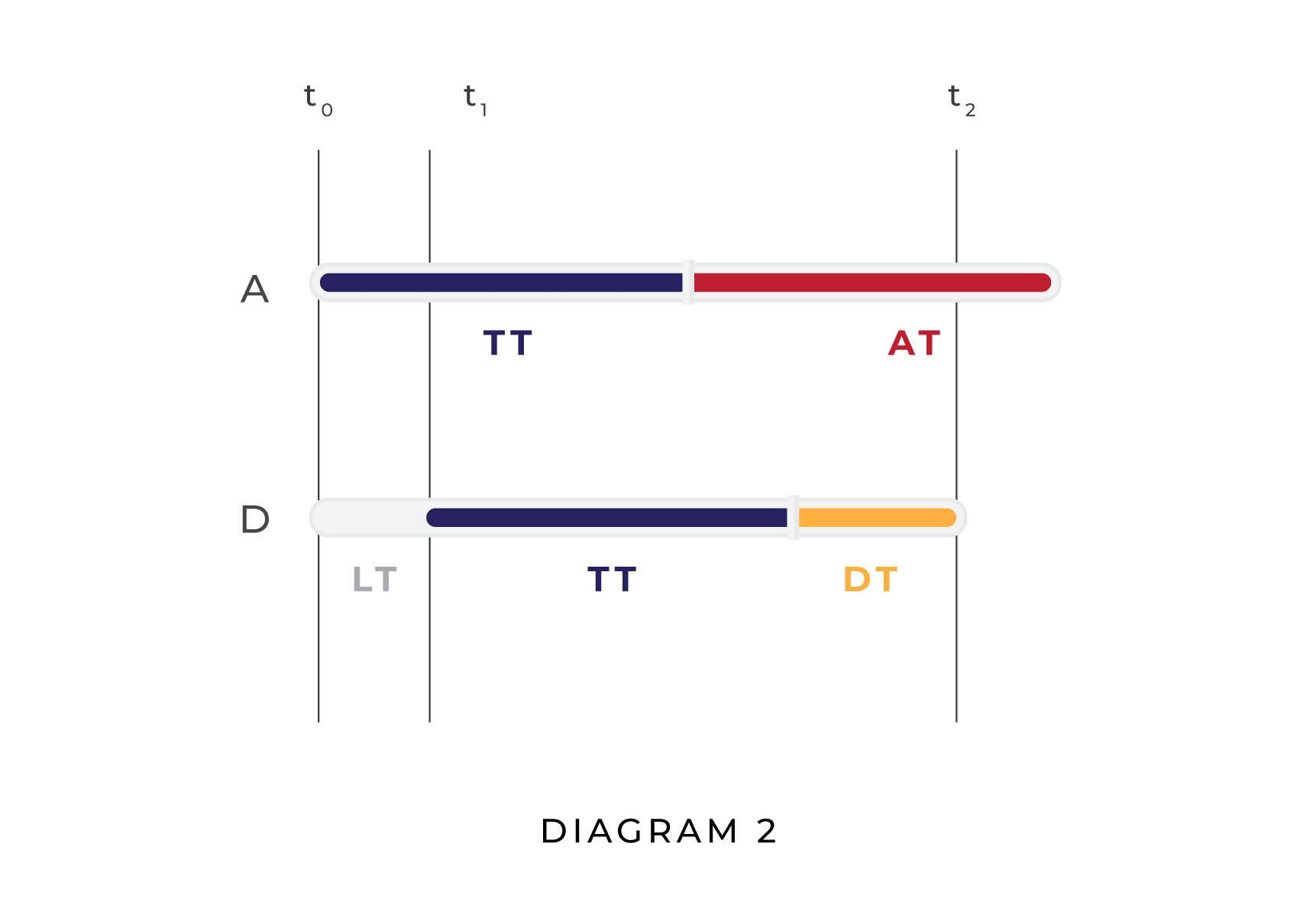
In Diagram 1, AT is greater than DT and LT is greater than AT, whereas in Diagram 2 AT is longer than LT, which is in turn longer than DT. Naturally, other relationships between AT, DT, and LT are possible; Diagram 1 and Diagram 2 do not represent the full range of possibilities. Their purpose is to show visually how, given our assumptions, whether a situation results in a unipolar scenario or a multipolar scenario is a function of LT, DT, and AT.
Note that the simple LAD model belongs to a broader class of conflict models. A variety of research has modeled conflicts in terms of ‘contest success functions,’ also known as ‘technologies of conflict’ (see, among others, Garfinkel and Skaperdas (2007), Fearon (2018), and Garfinkel and Dafoe (2019)). Contest success functions model whether a conflict will end in success, based on various input factors. For example, to model ground force invasions of a country, Garfinkel and Dafoe (2019) use a contest success function that takes as input the troop numbers for each side and outputs the number of troops that successfully make it through the border. The simple LAD model encodes a deterministic contest success function that maps attack, defense, and lag times to the deterministic states of success or failure, depending on whether AT is less than LT + DT.[7]
One of the unique features of our model, compared to models of other kinds of conflict, is its emphasis on lag time. A typical military decision about use of force involves weighing the relative strengths of the attacker and defender at a single time. But in the polarity problem, lag time gives the front-runner AGI a head start in deploying its resources.
4. Deploying the Simple LAD Model
Diagrams 1 and 2 depict how, given precise values for AT, DT, and LT, the simple LAD model predicts a unipolar or multipolar scenario. But we are not in an epistemic position to assign precise values to parameters like AT, DT, and LT. In order for the simple LAD model to be useful in practice, it needs to generate probabilities of unipolar or multipolar outcomes given probabilistic information about the values of AT, DT, and LT. This section introduces two ways to generate such probabilities.
First, we can place a lower bound on the probability of a unipolar outcome by assigning probabilities to hypotheses about the relationship between LT, AT, and DT. In particular, the simple LAD model predicts that a unipolar outcome results whenever DT > AT or LT > AT.
Consider DT > AT, the hypothesis that defense time is greater than attack time. The simple LAD model predicts that whenever this is true, the result is a unipolar outcome. After all, if the time it takes to mount a defense exceeds the time it takes to plan and execute an attack, the first AGI will be able to attack before the second AGI can defend, regardless of the value of LT. Even if A and D begin takeoff at the same time (the best possible scenario from D’s perspective), A will execute its attack before D has mounted a defense.
Now consider LT > AT, the hypothesis that lag time is greater than attack time. Again, this will result in a unipolar outcome, because the attacker will plan and execute its attack before the defender completes its takeoff.
Since AT, DT, and LT are continuous quantities, we assume that there is no chance that the values of any two of them are exactly equal. Given this assumption, we can partition the space of possible values for the three variables into the following six cells:
| AT > LT > DT | LT > AT > DT | DT > AT > LT |
| AT > DT > LT | LT > DT > AT | DT > LT > AT |
Shaded cells represent scenarios with a unipolar outcome.
Thus, by assigning probabilities to the various cells in the partition, we can arrive at a lower bound for the probability of a unipolar scenario by adding the probabilities assigned to the shaded cells.
For example, suppose you are confident that LT will be on the order of months, whereas AT and DT will be on the order of days, and you expect that DT will be roughly half of AT. Then your probability assignments might be:
| AT > LT > DT: .04 | LT > AT > DT: .70 | DT > AT > LT: .01 |
| AT > DT > LT: .04 | LT > DT > AT: .20 | DT > LT > AT: .01 |
Given these values, the simple LAD model places a lower bound of .92 on the probability of a unipolar scenario.
On the other hand, if you were confident that effective attacks take a long time to plan whereas effective defenses are quick and easy, and that lag time is not significantly longer than attack time or defense time, this method of using the simple LAD model would place a much smaller lower bound on the probability of a unipolar outcome.
The second way of using the simple LAD model to generate probabilities yields more precise predictions by assigning probability distributions over the possible values of AT, DT, and LT.[8] For example, assume that all three parameters are normally distributed random variables. As we have seen, the simple LAD model predicts that the probability of a unipolar scenario is equal to the probability that AT < DT + LT. This is equivalent to the condition that (DT + LT) - AT > 0. If DT, LT, and AT are normally distributed random variables, it is possible to calculate this probability by first using the formulas for adding and subtracting normally distributed random variables and then calculating the probability that the value of the resulting normally distributed random variable falls above 0. The probability of a multipolar scenario is then 1 - the probability of a unipolar scenario. The following table contains some examples of how the probability of a unipolar scenario depends on the distributions assigned to LT, AT, and DT.
| LT | AT | DT | Pr(Unipolar) |
| mean = 60; SD = 3 | mean = 6; SD = 1 | mean = 3; SD = 1 | ~1 |
| mean = 15; SD = 3 | mean = 30; SD = 3 | mean = 3; SD = 1 | ~0.003 |
5. Estimating Values for LT, AT, and DT
Deploying the simple LAD model requires assigning probabilities either to values for the parameters DT, AT, and LT or to the inequalities DT > AT and LT > AT. What probabilities would be reasonable to assign? In this section, we make the provisional case for assigning relatively high probabilities to both inequalities.
Which is likely to take longer, planning and executing an attack or a defense? One answer uses existing literature on cybersecurity. Cyber warfare is one of the main ways AI agents may compete against one another. A key concept here is offense-defense balance, which measures the relative ease of carrying out and defending against attacks. At least for small investments, work on cybersecurity suggests that the offense-defense balance tilts towards offense.[9] On the other hand, the balance may tilt towards defense as more resources are invested, in a phenomenon which Garfinkel and Dafoe (2019) call OD Scaling.
To see why the offense-defense balance favors the offense for low levels of investment, imagine that both the attacker and the defender are investing their resources in detecting vulnerabilities in the defender’s cyber infrastructure. An attack will succeed if it exploits one of the defender’s vulnerabilities which the defender has not detected and corrected. Now imagine that both the attacker and the defender invest enough resources to detect one vulnerability. This will only allow the defender to defend if the two have happened to detect the same vulnerability, which is unlikely. Only when enough resources have been invested by the defender to detect and correct most or all vulnerabilities is the defender likely to repel an attack.
In our model, offense-defense balance corresponds to the differential effect of investment on attack time versus defense time. If offense is favored, then investments decrease attack time faster than they increase defense time, meaning that DT > AT. In this way, an offense-defense balance that tilts to offense favors a unipolar outcome.
What about lag time?[10] Lag time depends in part on the ‘thickness’ of the market for AGIs. As the number of AGI efforts increases, the lag time decreases, since the ‘spaces’ in between levels of capability will be filled in (Bostrom 2014, 323). Another determinant of lag time may be the amount of discontinuity in AGI capability growth. If capabilities tend to grow in unpredictable jumps, there could be a large amount of time between the first AGI to make the ‘jump’ and the second.
6. Polarity Interventions for AT, LT, and DT
In this section, we propose some interventions that could increase the probability of a multipolar outcome by affecting attack time, defense time, or lag time. We will return to the question of safety-related interventions several times in what follows as our models become progressively more complex.
- Defense Head Start. The simple LAD model assumes that an AGI must plan and execute its own defense after finishing takeoff. If the human engineers leading AGI development projects allocated significant resources to detecting and patching the vulnerabilities in the systems they developed, however, this could give defenders a “head start,” reducing DT and increasing the probability of a multipolar scenario. One promising strategy might be to use AI to develop automatic patching of vulnerabilities (see Schneier (2018)).
- Increase Numbers. It might be possible to decrease LT by increasing the number of AGI efforts, filling in gaps in capability space.
- Limit Resource Access. If AGIs have access to fewer resources, then attack times (and potentially also defense times) will increase while lag times will stay the same. This lowers the chance that AT < DT + LT. For example, imagine that in a situation without resource scarcity, AT = 100, DT = 50, and LT = 51. Then the attacker beats the defender, resulting in a unipolar scenario. But now imagine that access to fewer resources would increase both attack times and defense times by 50%. In this resource-scare scenario, AT = 150, DT = 75, and LT = 51: the attacker would not be victorious over the defender, resulting in a multipolar scenario.
Because these interventions attempt to target AT, DT, or LT directly, they are likely to be relatively expensive, and the extent of their potential impact on polarity is unclear. A more promising strategy might be to intervene on AGI agents’ beliefs and values in a way that favors multipolar outcomes. To see how this might work, we must move beyond the simple LAD model.
7. Incorporating Expected Utility
In the simple LAD model, the decisions of the AGI actors are deterministic: attackers must attack and defenders must attempt to defend. But AGIs will ultimately make decisions based on their values and their uncertainty about the world. Even when attack time is less than defense time plus lag time, an AGI may not attack if it does not have a high enough confidence that its attack would succeed, or if it would be punished too severely in the event of failure.
We now develop models that represent an AGI’s values and uncertainty about attack time, defense time, and lag time. We imagine that each AGI has uncertainty about these variables and assigns utilities to the outcomes of its actions. In this section, we give up the automatic behavior assumption of the simple LAD model and develop the fixed role expected utility two-agent LAD model. In the next section, we give up the fixed roles assumption, resulting in the variable role expected utility two-agent LAD model.
In the fixed role expected utility two-agent model, each agent assigns probabilities to hypotheses about attack time, lag time, and defense time. We still assume fixed roles, positional awareness, and deterministic outcomes.
For example, here is one possible set of values for the subjective probabilities of an AGI attacker. Define victory as the condition where the attacking agent executes its attack and successfully disables the defender. Now imagine that the attacker has credences similar to our earlier example, where it is confident that LT will be on the order of months, whereas AT and DT will be on the order of days, and it expects that DT will be roughly half of AT.
| Victory | LAD Hypothesis | Pr |
| Maybe | AT > LT > DT | .04 |
| Maybe | AT > DT > LT | .04 |
| Yes | LT > AT > DT | .70 |
| Yes | LT > DT > AT | .20 |
| Yes | DT > AT > LT | .01 |
| Yes | DT > LT > AT | .01 |
Given its probability assignments, this attacker believes that the probability of victory conditional on it attacking is at least .92.
But probabilities aren’t everything. In this model, whether the attacker attacks also depends on how it values each of the following outcomes:
- The attacker attacks and achieves victory.
- The attacker attacks and does not achieve victory.
- The attacker does not attack.
An AGI attacker or defender must somehow combine its probabilities and values into a plan of action. To illustrate the relevant dynamics, we assume that AGI agents maximize expected utility. Given this assumption, an AGI attacker will decide what to do by calculating the expected utility of attacking vs not attacking.
What is the probability of a unipolar outcome according to this fixed role expected utility model? The model predicts that the probability of a unipolar outcome is equal to the probability that the first AGI chooses to attack and that either (i) AT < DT + LT (so that the defender could not have executed a defense at the time of the attack) or (ii) the defender decides not to defend. The probability that AT < DT + LT can be estimated using the methods described in Section 3. The probabilities that the attacker will attack and that the defender will defend depend on the beliefs and values of the two agents, as follows.
Consider first the attacker. Our fixed role assumption means that the attacker must perform one of two actions: it can attack, or it can refrain from attacking and pursue its other projects. If it attacks, one of two outcomes will result. Either it will succeed in disabling the defender, or it will not. The first of these outcomes results in a unipolar scenario, while the second results in a multipolar scenario. If the attacker refrains from attacking, the result is a multipolar scenario.
Let uA(attack with victory), uA(attack with failure), and uA(no attack) be the utilities the attacker assigns to the relevant outcomes. Let ND be the proposition that the defender does not plan and execute a defense. Then pA([AT < DT + LT] ∨ ND) is the attacker’s subjective probability that it will achieve victory if it attacks: this will occur just in case either the attack time is less than the sum of defense and lag time or the defender decides not to defend. It follows that the expected utility of attacking is equal to [pA([AT < DT + LT] ∨ ND) × uA(attack with victory)] + [(1-pA([AT < DT + LT] ∨ ND)) × uA(attack with failure)], and the expected utility of not attacking is equal to u(no attack). So the model predicts that:
- The attacker will attack iff [pA([AT < DT + LT] ∨ ND) × uA(attack with victory)] + [(1-pA([AT < DT + LT] ∨ ND)) × uA(attack with failure)] > uA(do not attack).
Now consider the defender. The fixed role assumption means that it must attempt to do one of two things: plan and execute a defense, or pursue its other projects. If it defends, one of two outcomes will result: either the attacker will attack before it is able to execute its defense, in which case the result will be a unipolar outcome, or the attacker will attack after it executes its defense (or not attack at all), in which case the result will be a multipolar outcome. If it chooses not to defend, the result will be a unipolar outcome just in case the attacker attacks. Let uD(successful defense), uD(unsuccessful defense), uD(no defense & not attacked) and uD(no defense & attacked) be the utilities the defender assigns to the relevant outcomes. And let NA be the proposition that the attacker does not plan and execute an attack. Then the expected utility of defending is equal to [pD([AT > DT + LT] ∨ NA) × uD(successful defense)] + [(pD([AT < DT + LT] ∧ ~NA)) × uD(unsuccessful defense)], and the expected utility of not defending is equal to [pD(NA) × uD(no defense & not attacked)] + [pD(~NA) × uD(no defense & attacked)]. So:
- The defender will defend iff [pD([AT > DT + LT] ∨ NA) × uD(successful defense)] + [(pD([AT < DT + LT] ∧ ~NA)) × uD(unsuccessful defense)] > [pD(NA) × uD(no defense & not attacked)] + [pD(~NA) × uD(no defense & attacked)].
Summarizing, our own credence in a unipolar outcome is equal to our credence that either: (i) AT < DT + LT and the attacker attacks, or (ii) the defender does not defend and the attacker attacks, where the probabilities that the attacker attacks and that the defender defends are determined by the probabilities we assign to the relevant propositions about pA, pD, uA, and uD.
8. Estimating Values for Probabilities and Utilities
We’ve already discussed how to think about the values of AT, DT, and LT. Our new model introduces extra variables: the AGIs’ own probabilities and utilities. Let’s consider what the values of these variables might be.
First, consider utilities. How might an attacker’s utilities for attacking and winning, attacking and losing, and refraining from attack compare to one another? If the attacker attacks and wins, it will be able to prevent the defender from reaching its level of capability and potentially interfering with its ability to promote its goals. So the attacker’s utility for attacking and winning will depend on the utility it assigns more generally to the achievement of its goals.
Now consider the utility of attacking with failure. Here, one possible cost for the attacker is economic sanctions from other AGIs. For example, imagine that each AGI has a comparative advantage in the production of some goods. In that case, an AGI which attacks and fails to achieve victory may face sanctions from the defender, being denied access to trade. Another possibility is that attacking with failure could lead to non-economic retaliation. On the other hand, if there is little gain from trade and little risk of retaliation, then an attacker that attacks and fails to achieve victory may not be worse off than an attacker that attacks and does achieve victory.
Finally, consider the utility for the attacker of not attacking at all. In a no-attack scenario, the attacker can be certain that the defender will continue to exist and pursue its goals, potentially interfering with the attacker’s ability to achieve goals. Moreover, the attacker faces the risk that the defender will eventually surpass it in capabilities and attack. This risk tends to decrease the utility of the no-attack situation. On the other hand, choosing not to plan and execute an attack leaves the attacker free to pursue other goals.
In general, as long as the attacker believes that the defender, if left to its own devices, will act in ways that make it more difficult for the attacker to achieve its goals, uA(attack with victory) will substantially exceed uA(attack with failure) and uA(no attack). Moreover, given that attacking with failure involves devoting resources to attacking rather than pursuing other goals, and given that a failed attack could result in sanctions, it seems likely that uA(no attack) will exceed uA(attack with failure). Together, these considerations suggest that
- uA(attack with victory) >> uA(no attack) > uA(attack with failure).
Turning from the perspective of the attacker to the perspective of the defender, we must compare the utilities of four outcomes: attempting to defend and succeeding, attempting to defend but not succeeding, pursuing other goals and being attacked, and pursuing other goals while not being attacked.
An immediate observation is that both attempting to defend and not succeeding and pursuing other goals and being attacked result in the permanent disempowerment of the defender. For this reason, these outcomes will have very low utility. Attempting to defend and succeeding and pursuing other goals while not being attacked both result in a multipolar scenario where the defender is able to pursue its goals. The main differences between the two outcomes are that (i) successfully defending insulates the defender from possible future attacks, and (ii) choosing not to defend allows the defender to allocate its resources to projects other than defense. Together, these considerations suggest that:
- uD(successful defense) ≈ uD(no defense & not attacked) >> uD(unsuccessful defense) ≈ uD(no defense & attacked).
What about credences? Here it is more difficult to say anything definite. If we think the first AGIs will have access to roughly the same evidence we do, we might expect their beliefs about AT, DT, and LT to be roughly the same as ours. If we think they will have radically less evidence or radically more evidence, on the other hand, we might expect their beliefs about AT, DT, and LT to be quite different from our own.
Despite our uncertainty about the credences a hypothetical attacker or defender might have, the fixed role expected utility two-agent model does allow us to make some observations. First, as the penalty associated with attacking with failure becomes less extreme, the likelihood that an attacker will attack increases. In the limit, if uA(attack with failure) = uA(no attack), an attacker will attack if it believes there is any chance it will succeed, since attacking is at least as good as refraining from attacking regardless of whether it succeeds.
Second, the conditions under which the defender will defend are more sensitive to the probability it assigns to AT > DT + LT than to the probability it assigns to NA, and defenders will defend when they assign even a relatively low probability to AT > DT + LT. To see this, consider the conditions under which the defender will defend rewritten with the simplifying assumption that uD(successful defense) = uD(no defense & not attacked) and uD(unsuccessful defense) = uD(no defense & attacked):
- [pD([AT > DT + LT] ∨ NA) × uD(successful defense)] + [(pD([AT < DT + LT] ∧ ~NA)) × uD(unsuccessful defense)] > [pD(NA) × uD(successful defense)] + [pD(~NA) × uD(unsuccessful defense)]
It follows from the theory of probability that pD([AT > DT + LT] ∨ NA) must be at least as great as pD(NA) and pD([AT < DT + LT] ∧ ~NA) must be no greater than pD(~NA). So the left-hand side of the inequality assigns more weight to uD(successful defense) and less weight to uD(unsuccessful defense) than the right-hand side whenever pD(AT > DT + LT) is nonzero. Given that uD(successful defense) >> uD(unsuccessful defense), this means the defender will defend.
Even under conditions of uncertainty, then, our model predicts that we should almost always expect attackers to attack and defenders to defend unless there is a substantial penalty for attacking without achieving victory.
9. Polarity Interventions on AGI Credence and Utility
We now list a few AI safety interventions that increase the chance of multipolar outcomes by affecting the relevant credences and utilities of AGIs.
Interventions on credences:
- Information Deprivation. If the attacker is very confident that AT < DT + LT, it will be likelier to attack. Since the standard view regarding cybersecurity is that AT < DT, we should expect AGIs to be somewhat confident that AT < DT + LT if they are epistemically competent and have access to adequate evidence. One possible polarity intervention would be to lower the attacker’s credence that AT < DT + LT by decreasing the amount of information that each AGI has about its opponent’s capabilities.[11]
Interventions on utilities:
- Reduce Incentives. The key benefit of attack for the attacker is the ability to pursue its goals without competition from the defender. Decreasing the attractiveness of a unipolar outcome compared to a power-sharing outcome therefore decreases the likelihood of an attack. One strategy here would be to give AGIs bounded utility functions. This in turn might involve imposing a high temporal discount rate, so that each AI values future events at a lower rate. In this way, the AGI could be designed so that the utility of unrestrictedly pursuing its goals is not very much higher than the utility of pursuing its goals while competing with other agents, since both plans will have similar outcomes in the short-term.
- Costly Failure. The main risk for an attacker is failure to achieve victory. Increasing the cost of attacking with failure will make attackers less likely to attack. For example, if there are benefits to a cooperative rather than adversarial relationship between the attacker and the defender, the attacker may prefer to guarantee a cooperative relationship by not attacking. As discussed above, there might be benefits to a cooperative relationship if each AI agent enjoys a comparative advantage in ways that produce trade. This in turn may be more likely if the space of AGIs is heterogenous.[12] There might also be benefits to a cooperative relationship if a failed attack would lead to long-term costly warfare between the attacker and the defender. It seems plausible that the cost of failure will increase as the number of AGI actors increases, since a failed attack on a single target could lead to sanctions from more parties.
Our general sense is that the safety interventions regarding AGI credences and utilities may be more feasible than safety interventions directly on AT, LT, or DT.
10. Incorporating Variable Roles
So far, we have assumed that the first AGI to complete takeoff is an attacker and the second is a defender. That is, we have assumed that the former does not consider defending and the latter does not consider attacking (we have called this assumption fixed roles). In this section, we extend the two-agent model to relax the fixed roles assumption.
As before, we assume that both agents are expected utility maximizers. However, we now allow both to choose between a broader set of available actions: attacking, defending, and pursuing other goals. Given this assumption, it is no longer appropriate to refer to the first AGI as the attacker and the second as the defender. Instead, we will refer to the first AGI as the leader (or for short) and the second as the laggard (or for short).
Both the leader and the laggard must now compare the expected utility of three acts rather than two. We focus first on the decision faced by the leader. Compared to the fixed roles model, the leader’s decision problem in the variable roles model is more complex in two ways. First, it must consider the possibility that the laggard will choose to attack. Second, it must consider the expected utility of defending as opposed to attacking.
For the leader, the expected utility of attacking is calculated just as in Section 7: attacking will result in victory if AT < DT + LT or does not defend, and failure otherwise. Note that if the leader chooses to attack, it does not need to worry about the possibility that the laggard also chooses to attack. This is because the leader is guaranteed to execute its attack first, meaning that, from the leader’s perspective, a situation in which both the leader and the laggard choose to attack is equivalent to a situation in which the leader attacks and the laggard neither attacks nor defends.
The leader’s expected utility for defending, however, raises new issues. If we assume that is defending and is attacking, rather than vice versa, the underlying causal structure changes so that the laggard’s attack succeeds iff AT + LT < DT. To see why, consider the diagram below:
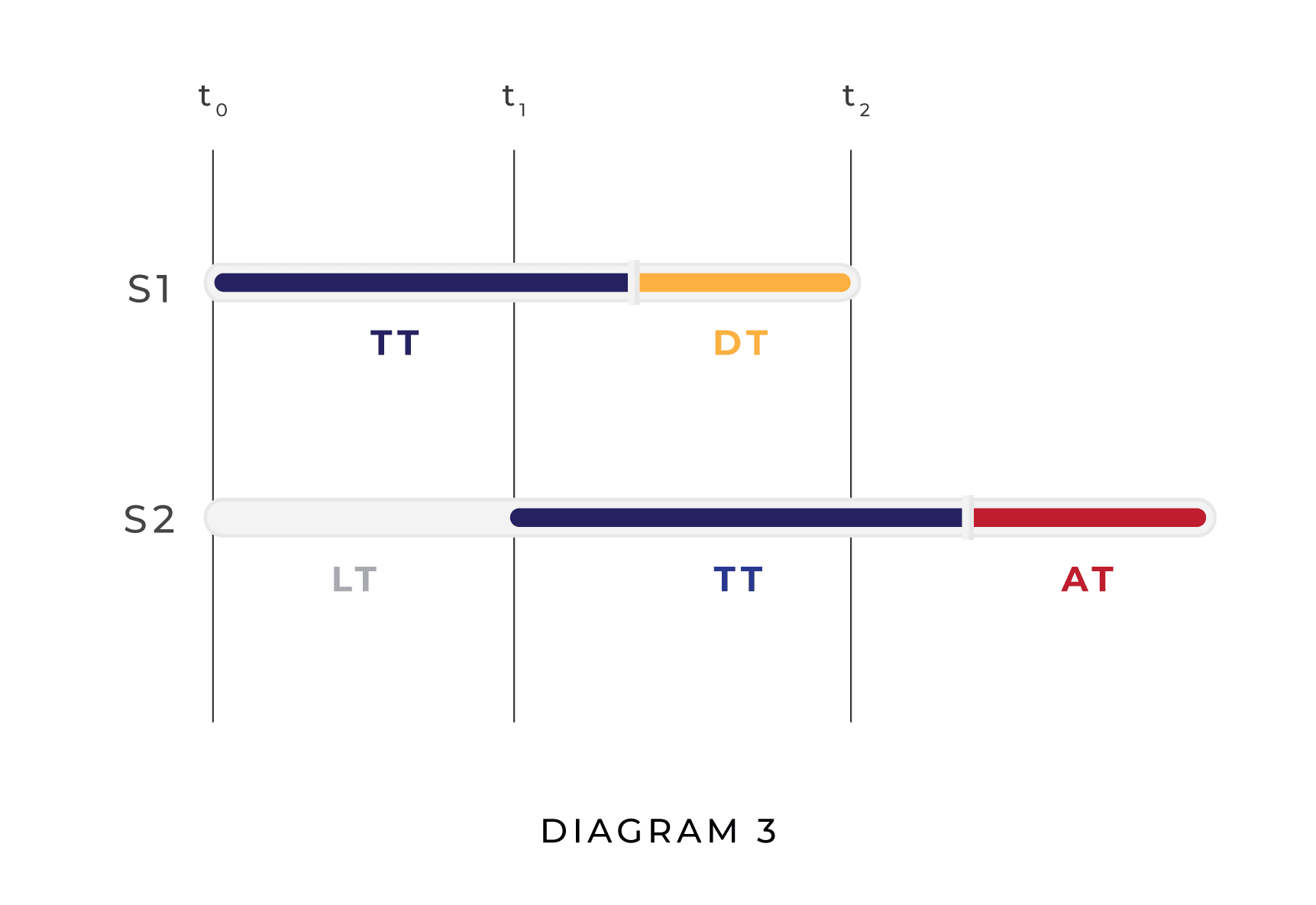
If the laggard decides to attack, the earliest time at which it can execute its attack is t0 + LT + TT + AT. The earliest time at which the leader can execute a defense, on the other hand, is t0 + TT + DT. So if the laggard attacks and the leader defends, the laggard’s attack will succeed just in case LT + AT < DT.
The leader’s expected utility for neither attacking nor defending depends on how likely it thinks the laggard is to attack. If the laggard defends or pursues its other goals, the leader is also free to pursue its goals. If the laggard attacks, however, then the leader is destroyed.
Here is a formal statement of the expected utility for the leader () of attacking, defending, and pursuing other goals. ND is the proposition that the laggard () does not defend. NA is the proposition that does not attack.
- Attack: [p([AT < DT + LT] ∨ ND) × u(attack with victory)] + [p([AT > DT + LT] ∧ ~ND) × u(attack with failure)]
- Defend: [p([DT < AT + LT] ∨ NA) × u(successful defense)] + [(p([DT > AT + LT] ∧ ~NA)) × u(unsuccessful defense)]
- Pursue other goals: [p(NA) × u(no defense & not attacked)] + [p(~NA) × u(no defense & attacked)]
We turn next to the laggard. Compared to the fixed roles model, the laggard’s decision problem in the variable roles model is more complex primarily in that it must now consider the expected utility of attacking as opposed to defending or pursuing other goals. When it comes to the expected utility of defending or pursuing other goals, we can simply copy the formulas from Section 7. To calculate the laggard’s expected utility of attacking, however, we must make two changes to the formula that applies to the leader. First, we must consider the probability that choosing to attack rather than defend will result in the laggard being left defenseless if the leader executes an attack. Second, as we saw, the victory condition for the laggard’s attack requires that AT + LT < DT. Formally, we have:
- Attack: [p(NA∧ ([DT > AT + LT] ∨ ND)) × u(attack with victory)] + [p([DT < AT + LT] ∧ ~ND) × u(attack with failure) + [p(~NA) × u(attack preempted)]
- Defend: [p([AT > DT + LT] ∨ NA) × u(successful defense)] + [(p([AT < DT + LT] ∧ ~NA)) × u(unsuccessful defense)]
- Pursue other goals: [p(NA) × u(no defense + not attacked)] + [p(~NA) × u(no defense + attacked)]
Informally, how does incorporating variable roles into the model change its predictions? A key observation is that both agents must now take into consideration more possible outcomes. From the leader’s perspective, for example, the possible benefits associated with attacking must be weighed against the security afforded by defending. And from the laggard’s perspective, the security afforded by defending might be outweighed by the prospect of a victorious attack.
We argued in Section 8 that uA(attack with victory) >> uA(no attack) > uA(attack with failure) and uD(successful defense) ≈ uD(no defense & not attacked) >> uD(unsuccessful defense) ≈ uD(no defense & attacked). Now we must consider how the leader or the laggard might rank all possible outcomes against each other. It seems clear that, for reasonable agents, u(attack with victory) will have the highest utility and u(unsuccessful defense) ≈ u(no defense & attacked) ≈ u(attack preempted) will have the lowest. This is because attacking with victory results in a unipolar scenario in which the agent is able to pursue its goals unimpeded, and being attacked with either an unsuccessful defense or no defense at all results in the agent’s destruction. Successfully defending, attacking without victory, and pursuing other goals without being attacked are all multipolar outcomes. Of the three, u(no defense & not attacked) is likely to be highest, since the agent is able to allocate resources towards its other goals rather than toward defense, while u(successful defense) and u(attack with failure) come slightly lower because both involve a long-term adversarial relationship between the leader and the laggard.
Ultimately, we think that giving up the fixed role assumption does not have a large effect on the strategic picture. Even though the leader can choose to defend, it is unlikely to do so, since the worst-case outcome of attacking (failing to achieve victory) is roughly as good as the best-case outcome of defending (successfully defending). Moreover, the fact that the laggard may attack lowers the leader’s expected utility for pursuing other goals. Similarly, even though the laggard can choose to attack, it is unlikely to do so. Unless it assigns a very high probability to the proposition that the leader will not attack, the risk of having its attack preempted will lead it to pursue other options.
For these reasons, we don’t think giving up the fixed role assumption reveals any significant new polarity affecting safety strategies. However, notice that the laggard in a variable roles model is especially disincentivized from attacking by the possibility of being preempted by the leader. This suggests that, if each AGI was uncertain about whether it was the leader or the laggard, both might be less likely to attack. We explore this possibility in the next section.
11. Incorporating Positional Uncertainty and Multiple Agents
Our models so far have made two simplifying assumptions:
- Positional Awareness. Each AGI is certain about whether it is the leader or the laggard.
- Number of Agents. There are only two AGIs engaged in strategic competition.
In this section, we discuss how to generalize our models to relax each of these assumptions. We focus on informal exposition of the changes required; logical details can be found in the appendices. As we will see, incorporating positional uncertainty and the possibility of multiple AGI agents shifts the expected utilities of all AGIs towards defending. This suggests two important new polarity interventions.
First, consider positional uncertainty. How do the dynamics of the polarity problem change when we imagine that, for all each agent knows, one of its opponents will complete takeoff before it and prepare an attack?
To approach this problem informally, recall that one upshot of our discussion in Section 10 was that when the laggard considers whether to attack, it must factor in the possibility that its attack plans will be preempted by an attack from the leader, resulting in its permanent disablement. This is the worst possible outcome from the agent’s perspective, and we should expect it to act so as to minimize its likelihood. This means defending rather than attacking or choosing to pursue its other goals.
When an AGI is uncertain whether it is the leader or the laggard, it will be less likely to attack, for two reasons. First, as an AGI’s credence that it is the leader decreases, its credence that its attack will succeed also decreases. This is because the laggard is at a disadvantage relative to the leader with respect to taking any action, since it is delayed relative to the leader by LT. This lowers the expected value of attack.
Second, as an AGI’s credence in leading goes down, its credence that it will be attacked goes up. This increases the expected value of not attacking, because it dramatically raises the value of mounting a defense. If it is attacked without a defense, it will be destroyed, and all of its plans will be frustrated. This is much worse than attacking with failure, and so should play a major role in any AGI’s decision making.
Let us turn now to the possibility of multiple agents. There are many companies currently working on developing AI systems. This could lead to a situation in which there are more than two AGIs released close enough to each other to engage in cooperative or adversarial behavior.
When we add the possibility of many agents into a model with positional uncertainty, the decision problem faced by each agent changes in two ways:
- When calculating the expected utility of attacking, the agent must consider whether it is likely to disable all, some, or none of the other agents in the model, and it must factor in the possibility that any agent that started takeoff before it will interrupt its plans with an attack.
- When calculating the expected utility of defending or pursuing other goals, the agent must consider the probability that any of the other agents in the model might attack it.
Both of these changes favor defending rather than attacking. Consider the first. The probability of achieving a high-utility unipolar outcome conditional on attacking goes down as the number of independent agents which would need to be defeated goes up. In fact, this happens in two different ways: First, increasing the number of defenders will tend to increase the time required to attack each defender. The attacker will have to divide its resources between each of its attacks. Second, increasing the number of defenders changes the task that the attacker must complete: each extra defender requires an extra AT < DT + LT condition for unilateral victory.
Now consider the second change. As the number of potential adversaries increases, each AGI faces more potential attacks which risk permanently disabling it unless it mounts a defense. This creates an additional incentive for defending rather than attacking.
Since unipolar victory requires defeating every opponent, the multi-agent model with positional uncertainty suggests that larger numbers of AGIs lead to lower chances of unipolarity. As before, our own credence that a given setup will result in a unipolar scenario is sensitive to our beliefs about all the attack, defense, and lag times as well as about what the various AGI agents themselves believe about the values of these parameters and the utilities they assign to different outcomes. Given that positional uncertainty in a multiple agent scenario incentivizes defending as opposed to attacking, however, one expects as a general rule that situations involving multiple agents and positional uncertainty will raise the probability of multipolar outcomes.[13]
12. Polarity Interventions for Positional Uncertainty and Multiple Agents
Incorporating positional uncertainty and increasing the number of agents both tend to disincentivize attacking relative to defending. This suggests a number of new interventions which might increase the probability of a multipolar outcome.
- Increase Positional Uncertainty. As each AGI becomes less confident of its position, it will become less likely to attack, increasing the chance of a multipolar outcome.
- Increase Heterogeneity. As the space of AGIs become more heterogeneous — meaning that the various AGIs have different kinds of vulnerabilities — it becomes more difficult for any given attacker to achieve victory over all of them. We can think of this in terms of a relationship between heterogeneity and the time it takes an attacker to plan attacks on each of its adversaries: as heterogeneity increases, AT increases, making victory less likely.
13. Conclusions and Future Directions
We have suggested a number of different possible interventions on the present or near-term course of AI development which could increase the probability of a multipolar scenario — an outcome which we have argued may be safer for humanity. But the fact that an intervention would increase the probability of a safer outcome conditional on the existence of at least one strategic, power-seeking AGI does not entail that it would increase the probability of a safer outcome, all things considered. By way of concluding, we discuss the likely all-things-considered impacts of each of our proposed interventions on human safety.
Recall our discussion in Section 2 of two ways in which humanity might avoid ever entering a situation in which the polarity problem becomes practically relevant: we might successfully resolve never to produce strategic, power-seeking AGIs, or we might institute effective mechanisms to detect and disable such AGIs before they are released and risk disempowering us. We have suggested above that increasing the number of AGI efforts increases the likelihood of a multipolar outcome by decreasing lag times. But increasing the number of AGI efforts also reduces the probability that humanity will successfully resolve never to produce strategic, power-seeking AGIs and increases the difficulty of the task of detecting and disabling AGIs that could disempower humanity. On balance, then, increasing the number of AGI efforts may not have an all-things-considered positive effect on human safety.
A similar point might be made about the idea of increasing the heterogeneity of the population of AGIs. While in a situation where AGIs have already been released increasing the heterogeneity of the AGI population might increase opportunities for profitable trade and decrease the probability that a single AGI will be able to successfully disable all its rivals, increasing the heterogeneity of the AGI population might also make it more difficult to use the same strategy to align different AGIs with human interests.
We are more confident that the other interventions we have discussed would increase the probability of a multipolar outcome without compromising human safety. This is likely true of increasing the costs associated with attacking with failure and increasing each AGI’s uncertainty about its opponents’ capabilities and its position as leader or laggard.
Some of the interventions we have suggested might even promote human safety independent of their impact on polarity. For example, the technological development required to achieve a defense head start — in particular, automated detection and patching of system vulnerabilities — could also be used to make it more difficult for a misaligned AGI to disempower humanity. Similarly, limiting resource access would slow down the pace of AGI research generally, giving humanity more of an opportunity to coordinate responses to safety risks, and limiting the payoff of achieving a unipolar outcome by producing systems with bounded utility functions could also reduce the probability of creating power-seeking AGIs in the first place.
In Section 3, we listed eight assumptions made by the simple LAD model. Above and in the appendices, we have shown how to generalize away from the first four of those assumptions. Here we briefly sketch how some others might also be lifted in future work, as well as the question of whether our model might be applied to possible future conflicts between AGIs and humanity.
A natural first step might be to abandon the assumption that each AGI effort has the same takeoff time and each AGI takes the same amount of time to plan an attack or a defense. One might be suspicious of this assumption, for example, if one thought that because alignment introduces additional constraints on a system, aligned systems suffer from an “alignment tax” which makes them slightly less capable than unaligned systems. The changes to the LAD model required to incorporate different takeoff, attack, and defense times are relatively minimal: we simply add more parameters to the model by indexing TT, AT, and DT to particular AGIs. The conditions which must be satisfied for a successful attack or defense can then be rewritten using these indexed parameters. While this approach would increase the detail of the model, one drawback would be that using the more detailed model to make predictions would require assigning probability distributions to more independent parameters. Our sense is that the versions of the model we present above strike the right balance between specificity and ease of use, but those who prefer more specificity can adapt them without difficulty.
One might also like to give up the deterministic structure of our model, wherein a specification of AT, LT, and DT produces a probability of either 1 or 0 that an attack would succeed. Here existing research on the economics of conflict may shed further light on the polarity problem. Work in that tradition relies on probabilistic contest success functions, which map initial expenditures of resources by a set of adversarial actors into a probability for each actor’s success, in terms of either the ratio or difference between resource expenditures (see for example Hirshleifer (1989), Konrad (2007)). This framework could help us model the effect of compute expenditures or relative capability on the probability of victory in a conflict between AGIs.[14] One way to integrate contest success functions into a LAD model would be to introduce a function from time elapsed since the beginning of an AGI’s takeoff to a quantity like capability or compute expended on attacking or defending, and then assign the probability that a given attack carried out at a time t will be successful in terms of the ratio or difference of the amounts of this quantity available to the attacker and defender at t. Extending the LAD model in this way would also allow for direct comparisons between the polarity problem and other types of conflict. Note that giving up the assumption of deterministic outcomes means also giving up on the idea, introduced in Section 3, that polarity dynamics do not depend on the shape of the takeoff process.[15]
A particularly important assumption made in the models we have discussed so far is that AGIs will not avoid conflict through bargaining.[16] This assumption may strike some readers as surprising, since those who study conflict often conclude that it imposes costs on both parties that could be avoided by bargaining, and that rational agents will always prefer bargaining to conflict for this reason. As Fearon (1995) points out, however, conflict may be rationally preferable to bargaining when certain conditions for the possibility of useful bargaining do not obtain. In particular, Fearon argues that conflict can be preferable to bargaining if (i) the relevant actors have private information (e.g. about their capabilities and what they would be willing to concede to avoid conflict) and incentives to misrepresent facts about this private information to each other, or (ii) actors cannot be trusted to commit to bargained outcomes because they have a strong incentive to violate bargains by attacking. It seems to us that both of these conditions for rational conflict are satisfied in cases relevant to the polarity problem. Unless AGIs are specifically designed with basic prosocial drives to tell the truth and abide by bargains with each other (in which case they are not expected utility maximizers), the laggard in a two-agent scenario has no reason to make bargained concessions to the leader, since after making the concessions the leader still stands to benefit from attacking. Indeed, if we relax the assumption of deterministic outcomes and assume that capability grows at least linearly with time, we should expect that the likelihood that the leader will prevail in a conflict remains constant or increases with time. This means that any tax the leader can impose on the laggard through bargaining will only increase its incentive to attack the laggard in the future.
But suppose we relax the assumption that AGIs will prefer conflict to bargaining. Perhaps in some scenarios in which there is much to be gained through trade, the leader might have incentives to abide by a bargained agreement with the laggard rather than attack. This would tend to favor a multipolar outcome.
We have also assumed that each AGI chooses how to act without information about how other AGIs have chosen to act.[17] This simplifies the models by abstracting away from cases in which, for example, the leader must consider how its decision about whether to attack will affect the probability that the laggard chooses to defend. Relaxing this assumption would involve distinguishing between various possible ways in which one AGI might be able to plan its actions in light of information about how another AGI has chosen to act and incorporating this kind of information into both AGI’s expected utility calculation. Suppose, for example, that it is common knowledge that the laggard will know whether the leader has planned to attack when it makes its decision about whether to defend. Then the leader must calculate the expected utility of attacking by considering the probability of ND (the proposition that the laggard does not defend) conditional on it attacking rather than the unconditional probability of that proposition, and the laggard will assign probability 0 to NA (the proposition that the leader does not attack) in its deliberation about what to do.
Finally, we have assumed a one-shot structure to the decision problems we consider. This assumption is reasonable if one thinks that the first interaction between any two AGIs is likely to decide the answer to the polarity problem: either one successfully disables the other, in which case we have a unipolar outcome, or this does not happen, in which case we have a multipolar outcome. Even if one thinks that temporally extended sequences of interactions can be relevant to polarity, modeling the structure of one-shot interactions between AGIs is an important first step towards a complete answer to the polarity problem. We regard generalizing models of the polarity problem away from the one-shot assumption as an important avenue for future research.
Might relaxing our assumptions in the ways just described result in a class of models which do not predict that the interventions we have recommended will change the probability of a multipolar outcome? We think this is unlikely. None of the generalizations of the LAD model we have considered seems likely to change the predicted impact of increasing the costs associated with attacking with failure, increasing each AGI’s uncertainty about its opponents’ capabilities and its position as leader or laggard, improving each AGI’s defensive capabilities, limiting resource access for all AGI efforts, or producing systems with bounded utility functions. So, though there are various ways in which the models we have proposed might be fleshed out or generalized, we remain confident in the lessons we have drawn from them.
A last question is whether our model can be applied to strategic interactions between AGIs and humans.[18] How might an AGI decide whether to attempt to disempower humanity? A natural thought might be that this sort of situation can be modeled using one of the two-agent LAD models developed above.
We think conflicts between AGIs and humans might be better modeled using existing frameworks from the economics of conflict literature, for two reasons. First, the central feature of the polarity problem which motivates the LAD model is that the temporal lag between AGI efforts gives AGIs which finish takeoff earlier a strategic advantage compared to AGIs which take off later. When thinking about interactions between humans and AGIs, there is no natural interpretation of the lag time or takeoff time parameters for human actors. Second, our way of thinking about conflicts between AGIs has been heavily influenced by the cybersecurity model. For example, this is what explains the idea that a successful attack could completely destroy an AGI and a successful defense could prevent all future attacks from succeeding. Disempowering humanity would likely require a conflict much more similar to a conventional war, and this kind of conflict is not naturally described using the LAD model.
References
Bostrom, N. (2014). Superintelligence: Paths, Dangers, Strategies. Oxford University Press.
Carlsmith, J. (2021). Is Power-Seeking AI an Existential Risk? Manuscript (arXiv:2206.13353).
Van Evera, S. (1984). The Cult of the Offensive and the Origins of the First World War. International Security 9: 58–107.
Fearon, J. D. (1995). Rationalist Explanations for War. International Organization 49: 379–414.
Fearon, J. D. (2018). Cooperation, Conflict, and the Costs of Anarchy. International Organization 72: 523–559.
Garfinkel, B. and Dafoe, A. (2019). How Does the Offense-Defense Balance Scale? Journal of Strategic Studies 42: 736–763.
Garfinkel, M. R. and Skaperdas, S. (2007). Economics of Conflict: An Overview. In Sandler, T. and Hartley, K. (eds.), Handbook of Defense Economics (vol. 2), Elsevier, pp. 649–709.
Hirshleifer, J. (1989). Conflict and Rent-Seeking Success Functions: Ratio vs. Difference Models of Relative Success. Public Choice 63:101-112.
Konrad, K.A. (2007). Strategy in Contests – An Introduction. WZB-Markets and Politics Working Paper No. SP II 2007-01.
Rescorla, E. (2005). Is Finding Security Holes a Good Idea? IEEE Security & Privacy 3: 14–19.
Schneier B. (2018). Artificial Intelligence and the Attack/Defense Balance. IEEE Security & Privacy 16: 96.
Slayton, R. (2017). What Is the Cyber Offense-Defense Balance? Conceptions, Causes, and Assessment. International Security 41: 72–109.
Lieber, K. (2015). The Offense-Defense Balance and Cyber Warfare. In Goldman, E.O. and Arquilla, J. (eds.) Cyber Analogies, Naval Postgraduate School, pp. 96–107.
Appendix 1: Positional Uncertainty
We can give a unified characterization of and ’s expected utilities for attacking and defending under conditions of positional uncertainty by introducing relativized lag times. In the simple LAD model, we had a single parameter LT representing the time which elapses between the beginning of the leader’s takeoff and the beginning of the laggard’s takeoff. In a two-agent model, we can introduce relativized lag times by adding two lag time parameters, LT and LT, representing the time which elapses between the beginning of ’s takeoff and the beginning of ’s takeoff (in the case of LT), or the time which elapses between the beginning of ’s takeoff and the beginning of ’s takeoff (in the case of LT). The idea of these new variables is that, while and must always believe that LT is positive because it represents the lag between whichever is the leader and whichever is the laggard, the values they assign to LT and LT can be either positive or negative, subject to the constraint that LT = -LT and one of the two must equal LT. For example, ’s beliefs about the value of LT encode its understanding of whether it is the leader or the laggard: assigning probability to positive values for LT indicates confidence that it is the leader, while assigning probability to negative values for LT indicates confidence that it is the laggard. The same is true, mutatis mutandis, for and LT. In conditions of positional uncertainty, each agent may assign some probability to a positive value for one of these variables and some probability to a negative value for the same variable, indicating ignorance about which agent is the leader. For example, may be certain that the gap between leader and laggard is 6 months, but be only 50% confident that it is in the lead. In that case, it will assign a probability of 0.5 to the proposition that LT is 6 months and a probability of 0.5 to the proposition that LT is -6 months.
Now we replace LT with with LT or LT in the inequalities used to calculate the utility of attacking. This gives us AT < DT + LT (for ) and AT < DT + LT (for ). For positive values of the relevant lag time variable (when the agent believes it is the leader), this inequality is equivalent to AT < DT + LT. For negative values of the variable, on the other hand, it is equivalent to AT + LT < DT . (To see this, note that when LT is negative, LT = -LT. It follows that subtracting LT from both sides of the inequality AT < DT + LT is equivalent to adding LT to the left side.)
All that is left is to incorporate the agent’s uncertainty about being attacked into the expected utility it assigns to attacking. Here, it is helpful to define what it takes for agent to defeat agent , depending on whether is leading or lagging behind :
- The leader victory condition is [AT < DT + LT] ∨ ND. Leader victory requires that either the attack time against is faster than the lag time plus the defense time; or decides not to defend.
- The laggard victory condition is NA ∧ ([AT < DT + LT] ∨ ND). Laggard victory requires that decides not to attack, and also that either ’s attack time against is faster than the (negative) lag time plus the defense time, or decides not to defend.
We can then represent an agent ’s uncertainty about whether it is leader or laggard by considering the probability it assigns to the disjunctive proposition that LT > 0 and the leader victory condition is satisfied or LT < 0 and the laggard victory condition is satisfied.
Incorporating positional uncertainty into our two-agent model gives us the following formulas for calculating the expected utilities of attacking, defending, or doing neither:
- Attack: [p((LT > 0 ∧ leader victory condition) ∨ (LT < 0 ∧ laggard victory condition)) × u(attack with victory)] + [p([AT > DT + LT] ∧ ~ND) × u(attack with failure)] + [p(LT < 0 ∧ ~NA) × u(no defense & attacked).
- Defense: [p([DT < AT + LT] ∨ NA) × u(successful defense)] + [(p([DT > AT + LT] ∧ ~NA)) × u(unsuccessful defense)]
- Pursuing other goals: [p(NA) × u(no defense & no attack)] + [p(~NA) × u(no defense & attacked)]
Appendix 2: Multiple Agents
Assume there are n AGIs, a1…an, ordered by age, and that each AGI agent makes a decision about whether to attack all of the other n-1 agents, defend, or pursue its other goals. Whether any AGI can achieve a unipolar outcome by attacking depends on whether it can achieve victory over every other AGI. Each attack and defense could in principle take a different amount of time, depending on the architecture of the defender. In addition, there is a lag time corresponding to each pair of AGIs.
We introduce n attack and defense time parameters ATi and DTi (1 ≤ i ≤ n), with ATi representing how long it takes an attacker to plan and execute an attack against the ith agent and DTi representing how long the ith agent will take after completing takeoff to plan and execute a defense. We assume that a completed defense enables an AGI to ward off attacks from all sources. We also introduce n2 relativized lag time parameters LTij (1 ≤ i,j ≤ n), where, from the perspective of a given agent i, LTij represents the time which elapses between the beginning of i’s takeoff and the beginning of j’s takeoff. (Thus if an agent i is certain it is the oldest such agent, it will assign positive values to each LTij where i ≠ j, whereas if it is certain it is neither the oldest nor the youngest, it will assign positive values to some LTij and negative values to others.)
For simplicity, we will assume that each agent in the model assigns the same utility to any multipolar outcome in which it is not disabled by another agent’s attack. This allows us to continue to speak of each agent’s utility for the outcome attack with victory (that is, the outcome in which it attacks and disables every other agent) and the outcome attack with failure (that is, the outcome in which it attacks but does not disable every other agent).
From the perspective of a given agent ai competing with agent aj, let’s again distinguish two victory conditions: what it takes for ai to defeat aj if ai is leading aj in the capability race, and what it takes ai to defeat aj if ai is lagging behind aj in the capability race:
- The leader victory conditionij is [ATj < DTj + LTij] ∨ NDj. In other words, this requires that either ai’s attack time against aj is faster than the sum of aj’s defense time and the lag between ai and aj, or aj decides not to defend.
- The laggard victory conditionij is NAj ∧ ([ATj < DTj + LTij] ∨ NDj). In other words, this requires that aj decides not to attack, and: either ai’s attack time against aj is faster than the sum of aj’s defense time and the (negative) lag between ai and aj, or aj decides not to defend.
Formally, we can incorporate the aforementioned differences into the two-agent model with positional uncertainty quantificationally, as follows:
- Attack: [pi(for all j (LTij > 0 ∧ leader victory conditionij) ∨ (LTij < 0 ∧ laggard victory conditionij)) × ui(attack with victory)] + [pi(for some j ([ATj > DTj + LTij] ∧ ~NDj) ∧ ~for some j (LTij < 0 ∧ ~NAj)) × ui(attack with failure)] + [pi(for some j (LTij < 0 ∧ ~NAj)) × ui(no defense + attacked)].
- Defend: [pi(for all j ([DTi < ATi + LTij] ∨ NAj)) × ui(successful defense)] + [pi(for some j ([DTi > ATi + LTij] ∧ ~NAj)) × ui(unsuccessful defense)].
- Pursue other goals: [pi(for all j (NAj)) × ui(no defense + not attacked)] + [pi(for some j (~NAj)) × ui(no defense + attacked)].
- ^
Carlsmith defines these terms as follows:
“A system engages in “agentic planning” if it makes and executes plans, in pursuit of objectives, on the basis of models of the world” (2021, 8)
“An agentic planner has “strategic awareness” if the models it uses in making plans are broad, informed, and sophisticated enough to represent with reasonable accuracy the causal upshot of gaining and maintaining different forms of power over humans and the real-world environment.“ (2021, 10).
- ^
For more on recursive self-improvement, see <https://www.lesswrong.com/tag/recursive-self-improvement>.
- ^
We understand the phrase ‘threats to human existence and wellbeing’ so that it includes both existential risks (X-risks) and risks of extreme suffering (S-risks), as well as other potential risks.
- ^
This assumption is encoded in our definition of ‘attack’ above.
- ^
See Section 13 for discussion of the suitability of this assumption in the context of the polarity problem and the effects of relaxing it.
- ^
Bostrom (2014, 103) suggests that polarity is also affected by a related factor: the shape of the takeoff process. He writes, ‘if the takeoff process is relatively slow to begin and then gets faster, the distance between competing projects would tend to grow.’ Elaborating, Bostrom argues:
‘Suppose it takes a project one year to increase its AI’s capability from the human baseline to a strong superintelligence, and that one project enters this takeoff phase with a six-month lead over the next most advanced project…Suppose it takes nine months to advance from the human baseline to the crossover point, and another three months from there to strong superintelligence. The frontrunner then attains strong superintelligence three months before the following project even reaches the crossover point. This would give the leading project a decisive strategic advantage.’
Care must be taken in interpreting Bostrom’s remarks here, since he uses the term takeoff slightly differently than we do. For Bostrom, takeoff begins when an artificial system with human-level general intelligence comes into being and ends when that system achieves superintelligence. Nevertheless, Bostrom’s argument applies equally to the takeoff process as we define it. Pace Bostrom, the simple LAD model predicts that the shape of the takeoff process does not affect polarity because it does not affect attack time, defense time, or lag time. Because it assumes deterministic outcomes, it predicts that the success or failure of an attack is not a function of the relative capabilities of the attacker and the defender. See Section 13 for discussion of how to relax this assumption of the simple LAD model. We believe it is an interesting question for further exploration whether the outcomes of adversarial interactions between AGIs are better modeled by assuming deterministic outcomes or by assigning probabilities of victory as a function of relative capability.
- ^
In other words, the simple LAD model encodes the function: f(AT, LT, DT) = 1 iff AT < LT + DT; = 0 otherwise.
- ^
Treating the variables as normally distributed means assigning a small but nonzero probability to the possibility that they take negative values, which is not conceptually possible for durations. This detail can safely be ignored as long as our purposes do not require us to make extremely precise predictions.
- ^
See e.g. Rescorla (2005), Lieber (2015), Garfinkel and Dafoe (2019). For a more skeptical approach, see Slayton (2017).
- ^
See Bostrom (2014, 102) for discussion of lag times across a historical range of technological races.
- ^
The idea that reducing the amount of information actors have about each other might prevent conflict may seem counterintuitive to some readers familiar with the idea, common in political science, that conflict can often be avoided if actors have complete information about their relative capabilities. However, this role of information in avoiding conflict is mediated by the possibility that parties are able to strike and abide by a bargain, and we have assumed that AGIs are not able to do this. See Section 13 for further discussion.
- ^
For a discussion of heterogeneity, see: https://www.lesswrong.com/posts/mKBfa8v4S9pNKSyKK/homogeneity-vs-heterogeneity-in-ai-takeoff-scenarios
- ^
This model could also be used to explore the sizes of different multipolar outcomes. Instead of just considering whether an outcome is unipolar, we could think about how many of the defenders are defeated by the attacker. We have suggested that multipolar outcomes are safer for humanity than unipolar outcomes. It is possible that this safety advantage is monotonic, so that increasing the number of AGIs in the multipolar case always increases the safety for humanity. Here, one further question would be how each AGI assigns utilities to ‘partial victories’. Perhaps incapacitating some key AGI-opponents would produce substantial rewards short of unipolar victory.
- ^
For example, let C1 and C2 represent the compute spent on conflict by the leader and laggard. Two hypotheses are (i) that the probability of the leader’s success is C1m / (C1m + C2m) for some m, or (ii) that it is 1 / (1 + ek(C2 - C1)), for some k.
- ^
Thanks to Jacqueline Harding for emphasizing this point.
- ^
Thanks to Dan Hendrycks for helpful discussion on this topic.
- ^
Thanks to Dmitri Gallow for helpful discussion on this point.
- ^
Thanks to Nate Sharadin for helpful discussion on this point.
