Note: Of reduced interest to generalist audiences.
Summary
I compiled a dataset of 206 mathematical conjectures together with the years in which they were posited. Then in a few years, I intend to check whether the probabilities implied by Laplace’s rule—which only depends on the number of years passed since a conjecture was created—are about right.
In a few years, I think this will shed some light on whether Laplace’s rule of succession is useful in practice. For people wanting answers more quickly, I also outline some further work which could be done to obtain results now.
The dataset I’m using can be seen here (a).
Probability that a conjecture will be resolved by a given year according to Laplace’s law.
I estimate the probability that a randomly chosen conjecture will be solved as follows:
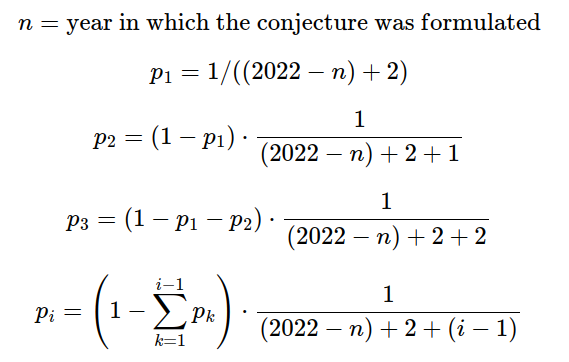
That is, the probability that the conjecture will first be solved in the year n is the probability given by Laplace conditional on it not having been solved any year before.
For reference, a “pseudo-count” corresponds to either changing the numerator to an integer higher than one, or to making n higher. This can be used to capture some of the structure that a problem manifests. E.g., if we don’t think that the prior probability of a theorem being solved in the first year is around 50%, this can be addressed by adding pseudo-counts.
Code to do these operations in the programming language R can be found here. A dataset that includes these probabilities can be seen here.
Expected distribution of the number of resolved conjectures according to Laplace’s rule of succession
Using the above probabilities, we can, through sampling, estimate the number of conjectures in our database that will be solved in the next 3, 5, or 10 years. The code to do this is in the same R file linked a paragraph ago.
For three years

If we calculate the 90% and the 98% confidence intervals, these are respectively (6 to 16) and (4 to 18) problems solved in the next three years.
For five years

If we calculate the 90% and the 98% confidence intervals, these are respectively (11 to 24) and (9 to 27) problems solved in the next five years.
For ten years

If we calculate the 90% and the 98% confidence intervals, these are respectively (23 to 40) and (20 to 43) problems solved in the next five years.
Ideas for further work
Do this experiment for other topics besides mathematical theorems and for other methods besides Laplace’s law
Although I expect that this experiment restricted to mathematical experiments will already be decently informative, it would also be interesting to look at the performance of Laplace’s law for a range of topics.
It might also be worth it to look at other approaches. In particular, I’d be interested in seeing the same experiment but for “semi-informative priors”—there is no particular reasons why that approach only has to apply to super-speculative areas like AI. So an experiment could look at experts trying to come up with semi-informative priors for events that are testable in the next few years, and this might shed some light into the general method.
Checking whether the predictions from Laplace’s law come true
In three, five, and ten years I’ll check the number of conjectures which have been resolved. If that falls outside the 99% confidence interval, I will become more skeptical of using Laplace’s law for arbitrary domains. I’ll then investigate whether Laplace’s law could be rescued in some way, e.g., by using its time-invariant version, by adding some pseudo-counts, or through some other method.
With pseudo-counts, the idea would be that there would be a number of unique pseudo-counts which would make Laplace output the correct probability in three years. Then the question would be whether that number of pseudo-counts is enough to make good predictions about the five- and ten-year periods.
Comparison against prediction markets
I’d also be curious about posting these conjectures to Manifold Markets or Metaculus and seeing if these platforms can outperform Laplace’s law.
Using an older version of the Wikipedia entry to come up with answers now
If someone was interested in resolving the question sooner without having to wait, one could redo this investigation but:
- Look at the List of unsolved problems in mathematics from 2015,
- checking to see how many have been resolved since then
- check whether adding pseudo-counts to fit the number of theorems solved by 2018 is predictive of how many problems have been solved by 2022
The reason why I didn’t do this myself is that step 2. would be fairly time intensive, and I was pretty fed up after creating the dataset as outlined in the appendix.
Acknowledgements

This is a project of the Quantified Uncertainty Research Institute (QURI). Thanks to Ozzie Gooen and Nics Olayres for giving comments and suggestions.
PS: You can subscribe to QURI's posts here, or to my own blog posts here.
Appendix: Notes on the creation of the dataset
I went through the list of conjectures on this Wikipedia page: List of unsolved problems in mathematics (a) and filtered them as follows:
- Ignored additional lists
- Ignore conjectures which have already been solved
- In cases where the date in which the conjecture was made, approximate it
- Ignore theorems without a full Wikipedia page or a large enough section in another page, as this would have made tracking down the date or tracking down resolution too difficult
- Ignoring the “Combinatorial games” section, as well as the many prime conjectures, as most were too short
- For problems that are equivalent, take the oldest formulation
- I sometimes ignored the case where a conjecture had been proven, and this led to even more conjectures
Note that if it turns out that a given conjecture was already solved by November 2022, it should be excluded from the dataset, rather than counted as a positive
I'm confused about the methodology here. Laplace's law of succession seems dimensionless. How do you get something with units of 'years' out of it? Couldn't you just as easily have looked at the probability of the conjecture being proven on a given day, or month, or martian year, and come up with a different distribution?
I'm also confused about what this experiment will tell us about the utility of Laplace's law outside of the realm of mathematical conjectures. If you used the same logic to estimate human life expectancy, for example, it would clearly be very wrong. If Laplace's rule has a hope of being useful, it seems it would only be after taking some kind of average performance over a variety of different domains. I don't think its usefulness in one particular domain should tell us very much.
I model a calendar year as a trial attempt. See here (and the first comment in that post) for a timeless version.
I think that this issue ends up being moot in practice. If we think in terms of something other than years, Laplace would give:
1−(1−1/(d⋅n+2))d
where if e.g., we are thinking in terms of months, d=12
instead of
1/(n+2)
But if we look at the Taylor expansion for the first expression, we notice that its constant factor is
1/(n+2)
and in practice, I think that the further terms are going to be pretty small when n reasonably large.
Alternatively, you can notice that
(1−1/(d⋅n))d converges to the n-th root of e, and that it does so fairly quickly.
Edit: This comment is wrong and I'm now very embarrassed by it. It was based on a misunderstanding of what the NunoSempere is doing that would have been resolved by a more careful read of the first sentence of the forum post!
Thank you for the link to the timeless version, that is nice!
But I don't agree with your argument that this issue is moot in practice. I think you should repeat your R analysis with months instead of years, and see how your predicted percentiles change. I predict they will all be precisely 12 times smaller (willing to bet a small amount on this).
This follows from dimensional analysis. How does the R script know what a year is? Only because you picked a year as your trial. If you repeat your analysis using a month as a trial attempt, your predicted mean proof time will then be X months instead of X years (i.e. 12 times smaller).
The same goes for any other dimensionful quantity you've computed, like the percentiles.
You could try to apply the linked timeless version instead, although I think you'd find you run into insurmountable regularization problems around t=0, for exactly the same reasons. You can't get something dimensionful out of something dimensionless. The analysis doesn't know what a second is. The timeless version works when applied retrospectively, but it won't work predicting forward from scratch like you're trying to do here, unless you use some kind of prior to set a time-scale.
Consider a conjecture first made twenty years ago.
If I look at a year as the trial period:
If I look at a month at the trial period:
As mentioned, both are pretty similar.
Apologies, I misunderstood a fundamental aspect of what you're doing! For some reason in my head you'd picked a set of conjectures which had just been posited this year, and were seeing how Laplace's rule of succession would perform when using it to extrapolate forward with no historical input.
I don't know where I got this wrong impression from, because you state very clearly what you're doing in the first sentence of your post. I should have read it more carefully before making the bold claims in my last comment. I actually even had a go at stating the terms of the bet I suggested before quickly realising what I'd missed and retracting. But if you want to hold me to it you can (I might be interpreting the forum wrong but I think you can still see the deleted comment?)
I'm not embarrassed by my original concern about the dimensions, but your original reply addressed them nicely and I can see it likely doesn't make a huge difference here whether you take a year or a month, at least as long as the conjecture was posited a good number of years ago (in the limit that "trial period"/"time since posited" goes to zero, you presumably recover the timeless result you referenced).
New EA forum suggestion: you should be able to disagree with your own comments.
Hey, I'm not in the habit of turning down free money, so feel free to make a small donation to https://www.every.org/quantifieduncertainty
Sure, will do!
I like this idea! Quick question: Have you considered whether, for a version of this that uses past data/conjectures, one could use existing data compiled by AI Impacts rather than the Wikipedia article from 2015 (as you suggest)?
(Though I guess if you go back in time sufficiently far, it arguably becomes less clear whether Laplace's rule is a plausible model. E.g., did mathematicians in any sense 'try' to square the circle in every year between Antiquity and 1882?)
I wish I had known about the AI Impacts data sooner.
As the point out, looking at remembered conjectures maybe adds some bias. But then later in their post, they mention:
Which could also be used to answer this question. But in their dataset, I don't see any conjectures proved between 2014 and 2020, which is odd.
Anyways, thanks for the reference!
I would have thought that "all conjectures" is a pretty natural reference class for this problem, and Laplace is typically used when we don't have such prior information - though if the resolution rate diverges substantially from the Laplace rule prediction I think it would still be interesting.
I think, because we expect the resolution rate of different conjectures to be correlated, this experiment is a bit like a single draw from a distribution over annual resolution probabilities rather than many draws from such a distribution ( if you can forgive a little frequentism).
I agree, but then you'd have to come up with a dataset of conjectures.
Yep!
I think that my thinking here is:
I agree. On the other hand, I kind of expect to be informative nonetheless.