Thanks to Tom Davidson, who improved the quality of this (quite critical!) piece substantially. Further thanks to Evie for making this post more positive-EV.

This post outlines the reasons I personally don’t update much on Davidson’s model of takeoff speeds.

• Section 1 provides an introduction to Davidson’s model. This can be skipped if you’re already familiar with the model.
• Section 2 introduces a counterintuitive result from the model.
• Section 3 looks into the model’s code in an attempt to explain the counterintuitive result, and evaluates whether this casts doubt upon the model more broadly.
• Section 4 criticizes certain “headline results” from the model.
• Section 5 discusses how robust Davidson’s model is to disagreements with its core assumptions, alongside implications for how we ought to interpret the model.
• Section 6 concludes.

Introduction

To begin our quick precis of Davidson’s model, we’ll provide two headline results.

1. By 2040, AIs will be able to (profitably) do every form of cognitive work that humans can currently perform.
2. AIs will automate 20% of all cognitive work by 2036, or thereabouts.

To understand what this means, some definitions. First, if an AI can perform at least as competently at any cognitive task people currently pay money for, we’ll call that system ‘an AGI’. ‘Takeoff’ is the interval between 20% automation, and the development of AGI. ‘Takeoff speed’ denotes the calendar time between developing AIs that automate 20% of human cognitive labor, and the development of AGI. Thus, Davidson thinks we will develop AGI by 2040, and the gap between 20% and 100% automation will be about 3.5 years.

Davidson gets the result from an augmented economic model, and specifically a semi-endogenous growth model. If the term ‘semi-endogenous growth model’ means nothing to you, that’s not a big deal — the details of such models aren’t particularly important for what follows.^[1] Still, it’s worth having a rough sense of how Davidson’s model produces its mainline results.

The model assumes, very intuitively, that we need both hardware and software to develop AIs. Fortunately, we have data on historical trends for both hardware and software progress. So, we can include projections, based on historical data, in order to forecast the rate of hardware and software progress within the model.

To produce hardware and software, we need both people and money. Nonetheless, the relationship between these variables and technical progress is complicated – twice as many researchers, for example, does not necessarily result in twice as much hardware or software progress. So, we also include a bunch of other variables to project hardware and software progress into the future, accounting for potential diminishing returns, delays in building fabs, and much more besides.

The model also assumes that current algorithms, or current software, are “good enough” to produce AGI, given some (potentially astronomically large amount) of compute. How much is good enough? It’s a free parameter in the model, but Davidson assumes 1e36 FLOP, in line with the Biological Anchors report. We should also note that – alongside estimates for the FLOP required to train a model which automates 100% of 2022-tasks – we have estimates for the FLOP required to run a model that automates 100% of 2022-tasks. Generally, it takes more FLOP to train a model (‘training requirements’) than to run that very same model (‘runtime requirements’). Davidson estimates the runtime requirements of a 1e36 model to be ~1.6667e16 FLOP.

We now introduce a prosaic mathematical fact. Because we’ve assumed that some amount of FLOP is sufficient to automate 100% of tasks, we know that some amount of FLOP is sufficient to automate x < 100% of tasks. The dynamics relating to automation within the model are straightforward: if it takes (say) 1e30 FLOP to automate 10% of human cognitive labor – and there’s enough available FLOP to run such models – then those tasks get automated, once someone produces a training run using 1e30 FLOP. When these tasks get automated, remaining human labor is immediately reallocated among the set of non-automatable tasks.

We can thus summarize the model’s dynamics in bullet-point form:

• Hardware and software progress continue to improve, leading to a greater degree of spending on AI training runs.
• When a training run using the necessary amount of FLOP is conducted, some proportion of labor gets automated, with human labor immediately reallocated among the set of non-automatable tasks.
• Once a sufficient fraction of cognitive labor gets automated (Davidson assumes 6%), investors are assumed to “wake-up” to AI’s economic potential, causing investments into AI to accelerate.
  • More money begets more progress, leading to faster rates of automation.
  • Moreover: as AIs get more capable, AIs themselves can evermore effectively contribute to the task of automating more tasks. This is another factor accelerating AI progress.
• Eventually, accelerated progress speeds up AI progress, and leads us to develop AGI. Thus, we automate 100% of all 2022 cognitive labor.

(Davidson’s own summary post can be found here, and the interactive model here)

Some Counterintuitive Results

Some results from Davidson’s model are counterintuitive, and warrant closer examination. To begin, though, we need to introduce one of the model’s key parameters: the effective FLOP gap. The effective FLOP gap represents the “ratio between the effective FLOP needed to [train an AI that can automate the most demanding cognitive task], and the 20% most demanding task.” The report talks about ‘effective FLOP’, or the amount of ‘effective compute’, rather than the amount of plain-old ‘compute’. This is based on the assumption that software progress may allow us to do more, or get more bang for our buck, per unit of physical compute.  

With that in mind, let’s now suppose (given some initial estimates for the parameters in Davidson’s model) I make a particular kind of update. First, we’ll suppose that I update towards believing that more compute is required to develop an AI that can automate 100% of human cognitive labor. However, let’s also suppose this doesn’t change my estimate of the compute required to automate 20% of cognitive labor. The update we’re imagining is solely an update about the compute required to automate the most difficult cognitive tasks. Differently put, we’re envisioning an update towards the distribution of compute requirements for automation being, for whatever reason, more ‘end-loaded’.^[2]

If we increase the compute required for 100% automation (‘AGI Training Requirements’), and alter the FLOP gap so as to hold the FLOP requirements 20% automation, we get the following results from Davidson’s model:

1. My update should lead me to expect that the “wake-up” period (the point at which AI automates 6% of cognitive tasks, leading to a subsequent acceleration of investment into AI) now arrives earlier.

2. If we instead update towards thinking that both 100% and 20% automation are more computationally demanding (and make no other changes), the time at which we achieve 6% automation (‘wake-up’) can still arrive sooner.^[3]

On the face of it, these results might seem surprising. Naively, one might expect that thinking the most difficult tasks are harder to automate — without making 20% more automation more difficult — shouldn’t make earlier automation milestones easier to achieve. Why, then, does increasing the FLOP required for 100% automation accelerate progress towards 6% automation, thereby resulting in an earlier influx of AI investment?

To resolve this puzzle, we’ll look at the model’s accompanying code.^[4] 

Doubts About Distributional Assumptions

So far, we’ve seen ‘AGI Training Requirements’, and the Effective FLOP Gap (hereafter ‘gap’). In Davidson’s playground, the distribution of FLOP requirements for automating x% of tasks is automatically computed from the values of these parameters.

Given particular values for our parameters, the underlying model constructs the distribution of automating x% of tasks from various automation quantiles, defined in the model’s underlying code.^[5] First, the code defines a parameter called unit — this is the seventh root of the effective FLOP gap. ‘Top’ refers to our estimate of AGI training requirements,^[6] and these two variables are used to define effective FLOP requirements for x% automation, for various x:

          100%: top,
          50%: top/(unit^4),
          20%: top/(unit^7),
          10%: top/(unit^8.5),
          5%: top/(unit^9.5),
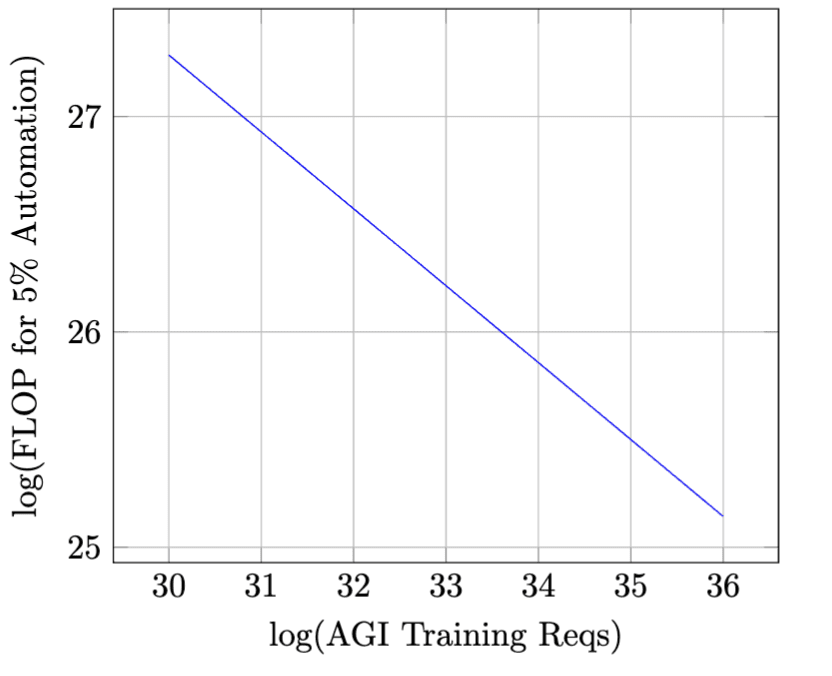
          0%: top/(unit^10.5).

The model’s code reveals a crucial dynamic, allowing us to explain our earlier results. If we alter ‘AGI training requirements’ while anchoring the FLOP requirements for 20% automation, this inevitably leads to a relative ease in automating tasks below the 20% threshold. The mathematical explanation is provided in this footnote.^[7] But I’ll also offer a few comments in the main text, with words and graphs, detailing how the code above helps explain our earlier results.  

Specifically, we’ll look at Figure 1. Here, the x-axis depicts increasing FLOP requirements for 100% automation, given a fixed value for 20% automation (I’ve arbitrarily set 20% automation equal to 1e28 FLOP). From the graph, we can see the following: as the FLOP requirements for 100% automation increase, the FLOP requirements for 5% automation (shown on the y-axis) decrease. And, importantly, the graph below depicts a general feature of Davidson’s model. If we hold 20% automation fixed, then any increase to ‘Top’ decreases the computational burden of automating tasks below the 20% automation threshold.

In terms of how these distributional assumptions might matter, concretely, let’s consider training requirements for different kinds of AI systems. 

1. In his report, Davidson notes that RL systems seem to require “several OOMs more training FLOP than similarly-sized LM” (Part 1, pg. 59), and notes a difference between GPT-1 and AlphaStar.
   1. Both AlphaStar and GPT-1 had a similar number of parameters (117 million vs 119 million), but GPT-1 took ~4 OOMs less compute to train than AlphaStar (1e19 vs ~2e23 FLOP).
2. Now, suppose that we make an update on the importance of training large Deep RL models for automating 100% of tasks, without making an update on the FLOP required to automate 20% of 2022 tasks.
   1. For instance, imagine that we previously believed that we could train LLMs without training deep RL systems, and thought this would be sufficient to automate 20% of 2022 tasks. If our faith in the ability of LLMs to automate 20% of cognitive labor remains unchanged, the FLOP requirements for 100% automation may increase while holding the FLOP required for 20% automation constant.
3. If we set Top: 1e36 → 1e39 and Gap: 1e4 → 1e7 while holding the rest of Davidson’s best-guess estimates fixed, the model now tells us to expect that we’ll automate 6% of tasks ~2.5 years sooner than we would have otherwise. Consequently, this leads to an influx of investments into AI ~2.5 years earlier than before.  

I don't offer this example because I have strong, inside-view estimates about the FLOP required to automate future tasks. Primarily, my issue is that Davidson’s report makes substantive (and largely implicit) structural assumptions about the nature of the world, which subsequently affects the model’s results. Specifically, Davidson assumes that – however else the world may shake out – all considerations implying an increased difficulty of crossing 20%-100% automation are considerations which, necessarily, lead to a decrease in the difficulty of automating earlier tasks. To the extent one doubts these implicit assumptions, the implied dynamics of the model won’t represent what one should expect to observe.

How Important Are the Distributional Assumptions?

Quite a bit, I think. There are both technical and conceptual points I want to make here.

My technical point is fairly simple: altering the automation distribution can significantly affect the model’s results. The conceptual point is a bit trickier, and will be made in Section 4. In short, though, I want to claim that disputes about the model’s distribution of FLOP requirements – while they might seem pernickety – illustrate a deeper, more general issue regarding the trust we should place in the model’s results.

Editing the Model

To illustrate the technical point, we’ll once again focus our attention on Davidson's automation distribution.

To avoid having the FLOP requirements for pre-20% automation depend on the gap between 20%-100% automation, I decided to fiddle with the model’s code. Combined with original automation distribution, Davidson’s best-guess estimates for AGI training requirements and the effective FLOP gap collectively imply certain FLOP requirements for each automation quantile. In turn, this allows us to back out effective multipliers on FLOP requirements for each quantile.^[8] The code below roughly captures Davidson’s originally implied ‘best-guess’ estimates of the FLOP required for each automation level, without dictating that automating x% of tasks (where x < 20) becomes comparatively easier when AGI training requirements increase while holding 20% automation requirements constant.

          100%: top,
          50%: (0.00508 * top) + (0.99492 * (top/gap))  
          20%: top/gap,
          10%: (top/gap) * 0.13895,
          5%: (top/gap) * 0.0372759,
          0%: (top/gap) * 0.01

With my updated distribution, FLOP requirements for x < 20% automation are fractions of the 20% level, and 50% automation requirements are a weighted average of the FLOP requirements 20% and 100% automation.

Still, we’ve not yet seen any reason to prefer my distribution to Davidson’s.^[9] To help compare these distributions, we’ll contrast my augmented code with Davidson’s original, in the context of two hypothetical stories. For ease of exposition, we’ll further assume that our initial estimates are identical to those in Davidson’s ‘best-guess’ parameter set.

• Story 1 (An End-Loaded Update): As before, we come to believe that scaled up transformers will be sufficient to automate 20% of tasks; but we update towards believing the need for larger RL training runs to reach 100% automation.
  • We add on 3 extra OOMs for 100% automation (=1e39), and hold the requirements for 20% automation fixed.

  • Under Davidson’s model, this results in 20% automation arriving earlier. With the augmented code, our update leaves earlier automation milestones unaffected.^[10] 

• Story 2 (Algorithmic Tricks): This time, we make an update on algorithmic progress. We now believe that 20% automation is achievable if GPT-4 had ~7 more OOMs of compute (~1e32 FLOP), with some “chain-of-thought-style trick” being likely sufficient to deliver 100% automation given that starting point (i.e., Gap ≈ 1).
  • According to Davidson’s model, this should lead you to expect wakeup to happen 3 years later, bring your timelines forward by a little over a year, and lead you to expect a takeoff of just over nine months.

  • According to my updated model, wakeup is unaffected (as 20% automation is held constant), timelines are brought forward by 3.4 years, and takeoff speed is similar (0.1 years longer).^[11]

If the distribution of automation requirements is relatively ‘end-loaded’ (Story 1), or if some clever algorithmic trick is sufficient to rapidly improve capabilities once AIs automate 20% of human labor (Story 2), then the model’s automation timelines will predictably be in error. Thus, the examples above help illustrate my more narrow, technical point: the model’s distributional assumptions struggle to capture alternative views about the future of AI, which are more naturally represented through adjustments to the model’s underlying structure.

Doubts About Headline Results

I now want to turn to a more conceptual question: a question about the preconditions necessary for trusting the results of a formal model.

To tackle the more conceptual question, I’ll investigate two of the model’s “headline results”. Then, I’ll claim these results only hold conditional on certain (unstated) assumptions about real-world dynamics, before closing with some remarks on models more generally.

The Relationship Between Takeoff and Timelines

Davidson offers one highlighted takeaway from his model: “Holding AGI difficulty fixed, slower takeoff → earlier AGI timelines”. This claim is offered as a takeaway even for those who “don’t buy the compute-centric framework”. It’s also a claim that admits of an uncontroversial reading, which can be stated precisely:

From Davidson’s model, it’s a deductive consequence that, if you increase the ‘effective FLOP gap’ parameter while holding all other parameters fixed, the point at which we develop AGI gets moved forward in time.

That claim, about deductive consequences, is uncontroversial — it’s a statement of the form “2+2=4, in Davidson’s model world”. From the more uncontroversial claim, though, we can ask a different, and more interesting question:

Given the deductive consequences of Davidson’s model, can we conclude that we have learned a fact about the relationship between takeoff speeds and timelines, holding AGI difficulty fixed? — a fact that we can expect to be generally true, not just in Davidson’s analogue world, but in the real world, too?

I don’t think so, at least if we’re interpreting the claimed relationship between takeoff speeds and timelines holding always, holding probably, or even holding with non-trivial probability.

From the model alone, we cannot say that “holding AGI difficulty fixed, slower takeoff → earlier AGI timelines” even with non-trivial probability,^[12] because of possible interaction effects between many real-world variables represented as independent parameters within the model, alongside dependence between model parameters and variables outside the model’s scope. The takeaway offered by Davidson only holds if: (i) “factors causing slower takeoff”, and (ii) “factors causing longer timelines” are independent, conditional on fixed AGI training requirements.

To illustrate this point, imagine that we start by agreeing with Davidson’s best-guess parameter estimates. Then, we update on the following (hypothetical) lines of evidence:

• Slower takeoff may be the result of automation bottlenecks impeding the degree to which AIs can “readily” automate certain tasks beyond the 20% threshold.^[13] 

  • With larger bottlenecks, you might also expect the substitutability of human labor in R&D to be higher. If there are large bottlenecks to automating more difficult tasks, then these bottlenecks may make it more difficult to substitute AI labor on Task 1 (which AIs can perform) for limited human labor on Task 2 (which humans still perform).

• Similarly, large bottlenecks to AI integration might make AI integration more costly, thereby making it less economically viable to have models with computationally expensive inference costs performing the relevant tasks.
  • In turn, this could affect your estimated tradeoff between training and runtime compute — there might only be demand for models which are far cheaper to buy, and thus far less expensive to run. Even if there’s a good theoretical case for the presence of this tradeoff for ML models, it might not apply in the context of AIs that (as the model assumes) actually contribute to economic automation.
• Finally, imagine that we make the updates above, without altering our estimate of AGI Training Requirements.
  • Perhaps our initial estimate of AGI Training Requirements priced in such bottlenecks eventually, and was set with such bottlenecks in mind. Now, we’re simply updating on the pervasiveness of such bottlenecks for automating less complex tasks.

Given the adjustments to Davidson’s best-guess estimates outlined in this footnote,^[14] updates towards slower takeoff can lead to later AGI timelines, even holding AGI difficulty fixed.

Admittedly, the result above follows from a particular set of parameter values, which one may or may not disagree with. Importantly, though, my objections are not focused on Davidson’s best-guess parameter values – I simply don’t think Davidson’s report licenses this headline result.

My objections about moving from model derivations to real-world claims hold even if you think the implicit dynamics encoded in Davidson’s model are good approximations for real-world dynamics. If the real-world factors represented in Davidson’s model are not (as a matter of real-world fact) independent, then claims about the real-world relationship between ‘takeoff’ and ‘timelines’ cannot be supported by observing the model’s outputs when one adjusts the parameters independently. This is because the claim “slower takeoff → earlier AGI timelines” contains a claim about the world’s modal structure. It says that if takeoff speed is lower, then AGI timelines are necessarily earlier, conditional on a fixed AGI difficulty.

However, if worlds in which I receive information rationally updating me towards slower takeoff are worlds in which other variables — variables which aren’t the training requirements for AGI — themselves vary across ‘fast takeoff’ and ‘slow takeoff’ worlds, then Davidson’s claim cannot be established from the results of his model. The only way to establish Davidson’s headline claim is to argue that (i) “factors causing slower takeoff”, and (ii) “factors causing longer timelines” are ~independent. As Davidson does not argue for the independence of (i) and (ii), I don’t think he can establish his claim from his model’s outputs.

Modal Robustness and The ‘Difficulty’ of Long Takeoff

Here’s another of Davidson’s suggested takeaways: “takeoff won’t last >10 years unless 100%-AI is very hard to develop”.

I think this claim could be interestingly precisified and debated. However, I don’t think it should (as Davidson suggests) be a conclusion we draw from “playing around with the compute-centric model”, and finding it “hard to get >10 year takeoff” in the absence of large FLOP requirements for AGI. Specifically, I think the real-world plausibility of “takeoff won’t last >10 years unless 100%-AI is very hard to develop” relies on a specific condition: before encountering the model, our prior probability for (Long Takeoff + Low Training Reqs) must have had most of its probability mass on specific worlds that are well-approximated by the dynamic structure assumed by Davidson’s model.^[15] 

Consider a concrete case, where a subset of ‘easy’ tasks are relatively straightforward to automate in practice, with bottlenecks on high-quality data fettering the automation of later tasks. Here, we might expect a subsequent downturn in AI investment to result in longer timelines — even if the ‘purely computational’ requirements of 100%-AI are not that high in principle.^[16] So, if we think that the world just described is plausible, it doesn’t seem as though Davidson’s model provides any reason to cast doubt on a world with both slow takeoff and (relatively) low training requirements.

Davidson’s summary post doesn’t consider such cases. However, he does provide the following argument.

“[Point 1.] AI progress is already very fast and will probably become faster once we have 20%-AI. If you think that even 10 years of this fast rate of progress won’t be enough to reach 100%-AI, that implies that 100%-AI is way harder to develop than 20%-AI.

[Point 2.]  …  today’s AI is quite far from 20%-AI: its economic impact is pretty limited (<$100b/year), suggesting it can’t readily automate even 1% of tasks. So I personally expect 20%-AI to be pretty difficult to develop compared to today’s AI.

[Therefore] … if takeoff lasts >10 years, 100%-AI is a lot harder to develop than 20%-AI, which is itself a lot harder to develop than today’s AI. This all only works out if you think that 100%-AI is very difficult to develop.”

The direction of justification for Davidson’s claims is unclear. If Points 1 and 2 are justified as a result of the model’s estimates, they don’t provide a non-circular defense of the model’s validity. Hence, we don’t have a response to the implausibility of cases like the imagined world above. Alternatively, if the claims in Davidson’s summary post are justified independently of the model, it’s unclear what that independent justification is meant to be. Indeed, some of the claims above are hard for me to evaluate in either direction (What do we mean when we say that 20%-AI is “way harder” than 100%-AI? From what starting point?).^[17]

Davidson, I think, raises an interesting hypothesis about the relationship between takeoff length and AGI training requirements. However, I think the worldview assumptions required for the hypothesis to be true are largely left implicit. Thus, I don’t think the report does much to support Davidson’s claim that “takeoff won’t last >10 years unless 100%-AI is very hard to develop”.

Headline Results and Models as Evidence

The underlying conceptual thread behind this section’s criticisms can be summarised as follows: in order to deliver claims about the real-world from model derivations, we need independent reasons to believe that the internal workings of the model combine our inputs in a way that is likely to be faithful to the actual dynamics governing how these variables interact in the real world.

In the present case, Davidon’s results should be treated as evidence about the real world only insofar as we think that assumptions implicit in Davidson's model world are assumptions that hold in the actual world.^[18] But, in order to make claims about the real-world on the basis of estimates derived from a model with particular parameter values, we need certain bridging premises. These ‘bridging premises’ are claims about what the abstract variables in the model are intended to represent, supported by arguments claiming that the dynamics assumed by the model are faithful to how these variables will actually interact in the real-world. For instance, we might want arguments for thinking that “causes of slower takeoff” and “causes of longer timelines” are ~independent,^[19] or arguments for thinking that other arguments for “>10 year takeoff & not-crazy-high AGI Training Reqs” are implausible.

For all the detailed and informative discussion about appropriate values for variables within the model, I don’t think the report clearly states or defends such bridging assumptions. Bridging assumptions we would need in order to move from: (i) estimates derived from the model with particular parameter values, and (ii) real-world claims about the arrival of AGI/ the length of takeoff. So, my primary source of skepticism about whether to update on the model’s results doesn’t come from disputes about particular parameter estimates, but deeper methodological doubts; it stems from an absence of arguments outlining why – or under what conditions – we should expect the model itself to be reliable. For that reason, that I’m skeptical about treating the model as a source of evidence about takeoff or timelines.

Interpretational Doubts

Introducing New Tasks

Davidson himself raises an interesting objection to his report. If automation creates new economic tasks, then the threshold for automating 100% of 2022-cognitive-labor doesn’t (generally) entail full automation when that threshold is met. However, the growth explosion dynamics arising from Davidson’s best-guess estimates are driven by the assumption that automating 100% of 2022 cognitive labor results in full automation. In response, Davidson offers the following “dodge”.

“If we think many important new tasks will be introduced that AI can’t perform, we can increase the degree to which automated tasks become less important (by decreasing the parameter ρ [the labor substitution parameter in the CES production function] and keep in mind that our training requirements for AGI (AI that can perform ~all cognitive tasks) should include any newly introduced tasks.” (pg. 87)

Suppose we bought Davidson’s dodge. That is, suppose we thought that new economic tasks (for which AIs were less well-suited) were likely to be introduced before all 2022-cognitive labor gets automated. And suppose, further, that we altered the previous parameter values based on our new interpretation of the parameters in question.

If we’re reinterpreting the parameters in Davidson’s model to fit with our new assumption, the dynamics encoded into the model do not just have to be invariant to plausible information that might affect our estimates of the relevant parameters, as standardly interpreted. Instead, the dynamics of Davidson’s model also have to be invariant to a swathe of reinterpretations of the parameters themselves. In effect, this means that justifying the usefulness of Davidson’s model requires responding to a super-charged variant of the Lucas Critique — the model would have to encode relationships that robustly held both between real-world variables represented in the model, and between de novo interpretations of the variables offered to make the model consistent with otherwise unmodeled dynamics.^[20] 

Under Davidson’s suggested reinterpretation, ‘AGI Training Requirements’ should now denote something like: “how much training FLOP will be required to produce the first AIs that collectively perform all cognitive labor in the human economy?”. Hence, under the new interpretation, ‘AGI Training Reqs’ (and so too the Effective FLOP Gap) will now be a function of time. Hence, if we’re using Davidson’s model to even represent a world where new, AI-unfriendly tasks get introduced, we’d have to engage in complex qualitative forecasting exercises prior to using the model. And, then, we’d have to compare the likely dynamics of our new world – the one where AI-unfriendly economic tasks are introduced – and compare the dynamics of that world against the model’s (already quite complex) dynamic assumptions. At the very least, I think the considerations above suggest a weak conclusion: certain recommendations for how to use the model are liable to generate misleading results.^[21] 

Perhaps counterintuitively, I think the weak conclusion holds precisely because the model captures so many potentially important dynamics for forecasting takeoff speeds.^[22] With a simple(r) model, it would be easier to check whether reinterpretations of the model’s parameters add up to an internally consistent world; in this case, the model would have more obvious domains of legitimate application, with more obvious scope and bounds. But, because Davidson’s model is so complex, it becomes much harder to ensure that any newly interpreted parameter values collectively result in something that looks like an internally consistent future — in light of how the old parameters were assumed to interact within its original imagined world. Thus, I also favor a stronger conclusion: if we expect novel economic tasks to be introduced, then we should simply claim that Davidson’s lacks practical utility, rather than attempting to save the model.

My case for favoring the stronger conclusion is straightforward. In simple terms, there just doesn’t seem to be any particular reason to believe that the dynamics of Davidson’s model would effectively capture a future in which new, less-automatable economic tasks are introduced.

‘Biased’ Estimates

Imagine that someone constructs a model for the amount of meals someone will eat next week. To do this, they multiply the number of children each person has by a random integer drawn from [0, 1e4]. And suppose, further, that this person engaged in a lengthy discussion about the potential “biases” of their estimator. They might acknowledge that, “if people’s hunger-levels increase next week, my estimator will underestimate the amount of meals they eat, as hunger would surely be a factor in cooking meals”. Or they might acknowledge that “if people are poorer next week, my estimator will overestimate the amount of meals they eat – less income, as we know, results in eating fewer meals”.

Davidson’s work, very obviously, contains far more valuable insight than the meal-consumption-model outlined above. But I think the caricatured situation above shares a notable similarity with Davidson’s project. Both Davidson and our caricatured modeler are primarily thinking of model limitations in terms of how omitted dynamics might bias their estimates in particular directions (Part 2, pp. 57-70). And, in both cases, I think that evaluations of the model’s directional biases are premature.

Specifically, I think it’s only fruitful to analyze the directional biases of a formal model once we have explicit assumptions connecting the model’s assumed dynamics to concrete, mechanistic claims about the assumed structure of the real-world. To make claims of bias, I think we need to know something about the sorts of worlds the modeling structure rules out, and what, concretely, the mathematical dynamics of the model assume about the real-world processes these dynamics are intended to represent. In our meal-consumption example, we need some justification for thinking that the model, at least roughly, manages to faithfully model the dynamics actually affecting meal-consumption. Likewise for Davidson. We need some justification for thinking that his model, at least roughly, manages to faithfully model a set of plausible futures for AI development.

To update on the results of Davidson’s model, I would personally want answers to the following question.

What, concretely, does the modeling structure itself assume about the world, and under which sorts of situations should we expect the model to be (un)reliable?

Here, there’s nothing special about the takeoff speeds model – I think any good model should have an answer to the question above.

If I’m considering whether to model some situation as Prisoner’s Dilemma, I’d consider whether there are at least two agents who care about different things, are (approximately) rational and for this to be common knowledge, etc. And, if these assumptions weren’t met, I’d treat that particular modeling structure as unreliable, and attempt to analyze the situation through other means. So, in a way, this point seems obvious. But (to my eyes) it also seems important. If we’re doing strategy, governance or policy, and the development of AI plays out radically differently than Davidson's model suggests – and we don’t carefully consider preconditions for the model’s reliability – then Davidson’s model would be worse than useless as a guide to policy and preparation; it would actively mislead us.

Conclusion

I want to acknowledge that this is a somewhat weird post to write.

For the most part, I’ve not actually disagreed with Davidson on claims directly related to AI. So I think it would be fair to wonder, at the end of all this, what the point of my post was – or what concrete, practical suggestions I'm hoping people will take away from what I've written.

My answer to “why write this?” rests on a couple of factors. First, it rests on sociology. I think headline results from large Open Phil reports function as an ‘intellectual center of gravity’ for a certain kind of person. When faced with a complicated mathematical model, and accompanying report spanning >200 pages, I think it’s easy for people’s estimates to get anchored around these headline results. Then, in turn, disagreements get translated into the language of said reports; estimates become ossified, with potential downstream influence on later policy work.  

The motivation for this piece also stems from shared concern about AI, and a hope that we can do AI forecasting better. Despite fairly deep disagreements with Davidson’s preferred methodological approach, I learnt a lot of cool information from reading the report; indeed, with some adjustments, there’s a version of Davidson’s mainline story holding a non-trivial vote share in my epistemic parliament. But, ideally, I’d like to engage in different sorts of discussions around AI forecasting. Discussions which place more focus on sketching out the possible narratives underlying formal models like Davidson’s, and providing arguments for and against these narratives.

I’ll close with nostalgebraist’s remarks on Biological Anchors, which echoes the sentiment of criticism expressed here:

“I think my fundamental objection to the report is that it doesn’t seem aware of what argument it’s making, or even that it is making an argument … [the report] sees itself … as computing an estimate, where adding more nuances and side considerations can only (it is imagined) make the estimate more precise and accurate. But if you’re making an estimate about a complex, poorly understood real-world phenomenon, you are making an argument, whether you know it or not.”  

1. ^{^}

   Also, good for you.

2. ^{^}

   Toy example: maybe we update towards thinking that automating high-quality data generation needed for training models to reliably reason about open-ended specialist tasks will require much more training FLOP.

3. ^{^}

   As an illustrative example, one can change the ‘best guess’ preset to have TrainReq = 1e39, and Gap = 1e7, corresponding to a situation in which AGI is more difficult, but the FLOP for 20% automation is unchanged; this brings forward wakeup by 2.4 years. Alternatively, if we start with Daniel Kokotajlo’s best-guess estimates and change TrainReq = 3e29 → 1e33, and Gap = 1e2 → 1e5, then the model also says that we should update towards expecting earlier wake-up (i.e., 6% automation). This is despite our only update from Kokotajlo’s views being an update towards thinking that both 20% and 100% automation are more difficult.

4. ^{^}

   The calculations discussed below can also be found in an accompanying spreadsheet to the report. Also, gratitude to Jaime Sevilla for directing me to the code, alongside offering to answer any of my questions; I didn’t take them up on the offer, but the kindness was not unnoticed.

5. ^{^}

   From the model’s quantiles, a full distribution is constructed through linear interpolation on the logarithm base 10 of the FLOP requirements.

6. ^{^}

   This function is also used to model runtime requirements, in addition to training requirements. Both ‘Top’ and ‘Gap’ admit different interpretations in that case.

7. ^{^}

    The FLOP requirements for each automation quantile are a function of ${\sqrt[7]{7\text{Gap}}}^n={\text{Gap}}^{n/7}$, for some fixed power $n$. If '$\text{Top}$' increases while the FLOP requirements for $20\%$ automation are held constant, then the numerator for $x\%$ automation gets multiplied by $C$, while the denominator gets multiplied by $C^a$, where $a>1$; this leads to lower FLOP requirements for $x\%$ automation given only a change to 100% automation difficulty level.

8. ^{^}

   This claim is complicated by the fact that Davidson’s original function constructs the distribution of both runtime and training requirements from ‘top’ and ‘unit’ variables, with the resultant values being different in each case. In order to more closely match the original distribution for both runtime and training requirements, one could alter the code in more substantive ways. I’ve opted against being too pernickety here, as Davidson himself seems to have constructed the distribution partly for convenience, and notes (contra the assumptions of the model+his best-guess parameter estimates) that he expects the FLOP gap between ~1%-20% automation to be “bigger” or “roughly as big” as the gap from 20%-100% (Part 1, pg. 82).

9. ^{^}

   There are also drawbacks to my approach. Under my modification, changes to the 20-100% gap won’t affect the gap between 10-20% automation at all. But you might think that “if tasks are bunched together after 20% then, all things equal, they should be more bunched together before 20%” [h/t Davidson]. Still, I take it that the effective FLOP gap is introduced as a separate parameter precisely because we might expect a difference between the degree to which tasks are “bunched together” across different automation milestones. In any case, the point of modifying the code is not to show that we should replace Davidson’s assumptions with my own, but merely to highlight assumptions of the model that may not be immediately transparent from casual inspection.

10. ^{^}

    Additionally, takeoff now takes 11 years, rather than the ~8.6 years suggested by plugging the updated parameters into Davidson’s original model.

11. ^{^}

    Perhaps worth noting is that, through adjusting the multipliers to fit Davidson’s reported views about the FLOP gap between ~1%-20% automation being ~“roughly as big” as the gap from 20%-100%, his new timelines reduce by a little over 2 years.

12. ^{^}

    For brevity, I will sometimes drop the qualifier ‘holding AGI difficulty fixed’ going forward, though it should be assumed present unless otherwise stated.

13. ^{^}

     ​In Davidson’s terminology, AIs can “readily” automate tasks when it is “profitable for organizations to do the engineering and workflow adjustments necessary for AI to [with one year of concerted effort from organizations making AI workflow integration a top priority] perform the task in practice.”

14. ^{^}

    Effective FLOP Gap: 1e4 → 1e7, and Labour Substitution R&D: -0.5 → -1.25. Also, remove the tradeoff between training and runtime compute. This is done with the standard version of Davidson’s model, and can be replicated in the playground.

15. ^{^}

    In practice, many people may not have thought through the dynamics with sufficient granularity, and may not be assigning probability mass to worlds that they’ve already considered (thanks to Davidson for this point). However, I think that this makes the epistemic situation of those updating on Davidson’s claims even more precarious. If you update on the model’s results and haven’t thought through specific worlds, then this makes one more liable to treating Davidson’s model as de facto capturing the key dynamics of AI automation, without sufficient attention to ways in which the model itself may encode assumptions which, on reflection, you’d disagree with.

16. ^{^}

    Alternatively, we might expect corresponding inefficiencies in the reallocation of human labor as AI gets more powerful: early LMs may allow people to spend more time on other tasks (part 2, pg. 70), with allocative inefficiencies becoming more severe for harder tasks. If difficulties reallocating human labor grow more prominent as automation ratchets up, more tasks may be introduced in this period for which humans are comparatively advantaged.

17. ^{^}

    As a smaller point, AI progress since the publication of Davidson’s report makes Point 2 seem more contestable.

18. ^{^}

    If we don’t think Davidson’s model world captures key dynamics occurring in the actual world, then we don’t have reason to believe that the model is more likely to output (say) “takeoff speed of ~3 years” in worlds where takeoff speeds are ~3 years.

19. ^{^}

    Conditional on fixed AGI training requirements, of course.

20. ^{^}

    Concrete example. In a world where new economic tasks are introduced, Davidson’s suggested reinterpretation of ‘AGI Training Requirements’ should now denote something like: “how much training FLOP will be required to produce the first AIs that collectively perform all cognitive labor in the human economy?”.

    Now, if timelines are very short and takeoff is fast, then AGI Training Reqs is plausibly similar to “100% automation of 2022-labor”. But, if timelines are longer or takeoff is slower, then your estimate of ‘AGI Training Reqs’ will to a large degree depend on already possessing a story about the events Davidson’s model attempts to forecast. For instance, it will require an answer to the question: “how much FLOP will it take to train AIs that can collectively (‘readily’) automate all cognitive labor in the human economy, given all the cognitive tasks that will exist when AGI is in fact developed?”

21. ^{^}

    Kokotajlo suggests going “through the top 5-10 variables [of the model] one by one and change them to what you think they should be (leaving unchanged the ones about which you have no opinion) …  [to see] what effect each change has”.

22. ^{^}

    This point is articulated much more cleanly thanks to critical feedback from Davidson; I expect he disagrees with it.