[This post has been published as part of draft amnesty week. I did quite a bit of work on this post, but abandoned it because I was never sure of my conclusions. I don't do a lot of stats work, so I could never be sure if I was missing something obvious, and I'm not certain of the conclusions to draw. If this gets a good reception, I might finish it off into a proper post.]
Part 1: Bayesian distributions
I’m not sure that I’m fully on board the "Bayesian train". I worry about Garbage in, garbage, out, that it will lead to overconfidence about what are ultimately just vibes, etc.
But I think if you are doing Bayes, you should at least try to do it right.
See, in Ea/rationalist circles, the discussion of Bayesianism often stops at bayes 101. For example, the “sequences” cover the “mammaogram problem”, in detail, but never really cover how Bayesian statistics works outside of toy examples. The CFAR handbook doesn’t either. Of course, plenty of the people involved have read actual textbooks and the like, (and generally research institutes use proper statistics), but I’m not sure that the knowledge has spread it’s way around to the general EA public.
See, in the classic mammogram problem (I won’t cover the math in detail because there are 50 different explainers), both your prior probabilities, and the amount you should update, are well established, known, exact numbers. So you have your initial prior of say, 1%, that someone has cancer. and then you can calculate a likelihood ratio of exactly 10:1 resulting from a probable test, getting you a new, exact 10% chance that the person has cancer after the test.
Of course, in real life, there is often not an accepted, exact number for your prior, or for your likliehood ratio. A common way to deal with this in EA circles is to just guess. Do aliens exist? well I guess that there is a prior of 1% that they do, and then i’ll guess likliehood ratio of 10:1 that we see so many UFO reports, so the final probability of aliens existing is now 10%. [magnus vinding example] Just state that the numbers are speculative, and it’ll be fine. Sometimes, people don’t even bother with the Bayes rule part of it, and just nudge some numbers around.
I call this method “pop-Bayes”. Everyone acknowledges that this is an approximation, but the reasoning is that some numbers are better than no numbers. And according to the research of Phillip Tetlock, people who follow this technique, and regularly check the results of their predictions, can do extremely well at forecasting geopolitical events. Note that for practicality reasons they only tested forecasting for near-term events where they thought the probability was roughly in the 5-95% range.
Now let’s look at the following scenario (most of this is taken from this tutorial):
Your friend Bob has a coin of unknown bias. It may be fair, or it may be weighted to land more often on heads or tails. You watch them flip the coin 3 times, and each time it comes up heads. What is the probability that the next flip is also heads?
Applying “pop-bayes” to this starts off easy. Before seeing any flip outcomes, the prior of your final flip being heads is obviously 0.5, just from symmetry. But then you have to update this based on the first flip being heads. To do this, you have to estimate P(E|H) and P(E|~H). P(E|H) corresponds to “the probability of this flip having turned up heads, given that my eventual flip outcome is heads”. How on earth are you meant to calculate this?
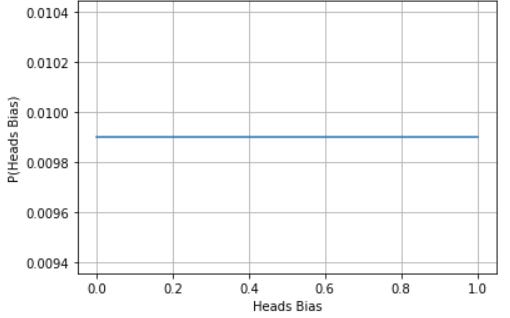
Well, the key is to stop doing pop-bayes, and start doing actual bayesian statistics. Instead of reducing your prior to a single number, you build a distribution for the parameter of coin bias, with 1 corresponding to fully biased towards heads, 0 being fully biased to tails, and 0.5 being a fair coin. With unknown information, you could use a “uniform prior”, where each value of bias between 0 and 1 is equally likely.
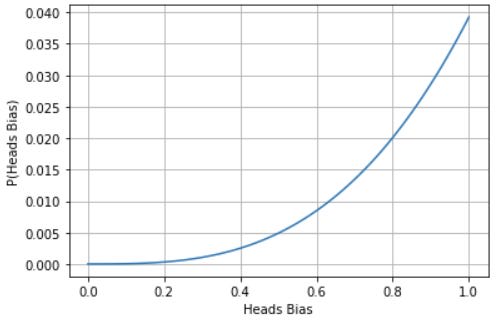
When a flip happens, we use bayes theorem not once, but many times, for each potential value of bias. In this case, the P(E|H) is now: what is the probability of seeing this heads result, given that the coins bias is this value? Clearly, this is higher for higher coin biases. If we do this 3 times, we get a new distribution like the following:
When the time comes, how do we convert this into a probability we can bet with? We can do an expected value calculation, multiplying the probability mass of each slice by it’s bias towards heads. In this case, that would add up to an 80% probability of getting heads next time.
What’s actually happening here is that we are splitting our uncertainty into two pieces: the uncertainty of what the true facts about the world are, and the uncertainty about the future, given those facts. Perhaps to an omniscient being, the two are one and the same, but we are not omniscient beings, and at least in this scenario, this split works beautifully.
Importantly, when modelling this problem, the thing we keep track of is the distribution. If we’ve seen the 3 heads, we don’t memorize “80%” and then throw away the distribution, because what happens if we see another flip?
With this, you can see that a statement like “I have a 95% credence that the bias is between X and Y” makes perfect sense. But remember, the “bias parameter” is simply the probability that the next flip is heads! So it also makes sense to say “I have a 95% credence that the “true” P(heads) is between X and Y”, although perhaps you would admonish someone saying this for using confusing language.
Okay, hopefully I’ve convinced you that probability of probabilities makes sense for a coin bias. But can you apply this to something like P(doom)?
Imagine Harriet is undecided between several models of the world. Specifically, she can’t decide how dangerous AI is. (the following are simplified models, not meant to give the actual case for each camp).
She considers model 1: the super-doomer model. In this model, intelligence is infinitely scalable, and some form of FOOM is inevitable, and will lead to murderous AI. Extremely high intelligence also can invent massively powerful tech within days or months, so defeat is inevitable, and nobody will be able to stop it coming into existence.. In this scenario, it doesn’t really matter what humanity does, the chance of humanity dying is still almost 100%.
But there is also model 2: the cautious optimist. This view says that FOOM can’t happen, but that near AGI will be very powerful, and some of them could be in the hands of malevolent actors. However, since development is slow, there is a high chance of “warning shots”, which would lead to constraints on AI that prevent disaster. If this view is true, then there is a good chance of survival, but we could still get wiped out if enough things go wrong at once, so there is maybe a 1% chance of doom.
And lastly there is model 3: the total AI skeptic. The total AI skeptic thinks we are in just in another hype cycle, like the ones preceding other AI winters. GPT is just a stochastic parrot, and will be forever plagued with hallucinations, and true AGI is still a century away. In this case, the chance of AI doom is like 1 in a trillion, and come from truly dumb scenarios like someone hooking GPT up to the nuclear launch codes.
Can you see? This is just the coins all over again. We split the uncertainty into uncertainty about the facts of the world, and uncertainty about what will happen when we “roll the dice”, given those facts.
5% on model 1, 70% on model 2, and 25% model 3. If we do an EV point estimate of the full P(doom), we would get 5.7%, with the bulk of that coming from model 1. More on that later.
These worlds are quite broad, and we can further split them into sub-worlds. For example, she could think three variant “sub-models” of model 2 are equally likely: ones in which the safeguards on bioweapons and nuclears are low, medium, or high security, with each model having slightly different chance of doom.
Now if Harriet encounters a news article on vulnerabilites in world security, she can shift among these sub-models, placing more weight on the more deadly ones. Note that this will have barely any effect on the other two models. This is the advantage of keeping track of the distributions and models: they can be updated individually.
Now that we’ve figured out how to apply bayesian distributions to a question like P(doom), let’s see what happens when you take this to the extreme, with a scenario I’ll call the “humble cosmologist paradox”
Part 2: the humble cosmologist paradox
An intrepid EA journalist is investigating possible sources of existential risk, and decides to look at the risk of “simulation shutdown”. The case goes that our world may be a simulation by our descendants, as argued in Bostroms “simulation argument”, or a simulation by higher beings (for example, as part of a science experiment). If this is true, all intelligent life in our simulation is at risk of being deleted forever, if the simulators find us to no longer be interesting or useful for our purposes.
To answer this question, the journalist secures an interview with a successful cosmologist, noted for his humble nature.
Journalist: What is your P(doom) from simulation shutdown?
Cosmologist: “Unfortunately, there is almost nothing I can tell you here. For example, the prospect of higher beings is an unfalsifiable one: it could be that in a higher universe, computation is incredibly fast and easy, or only certain aspects of our world are being simulated. Given that simulations are possible in our world, I can’t rule it out as impossible. I think the only sensible answer I can give is “I don’t know.”
Journalist: I expect a large amount of uncertainty. I’m just asking you to quantify that uncertainty. For example, you’ve just said that you “can’t rule it out”. That implies you know something, which can be quantified.
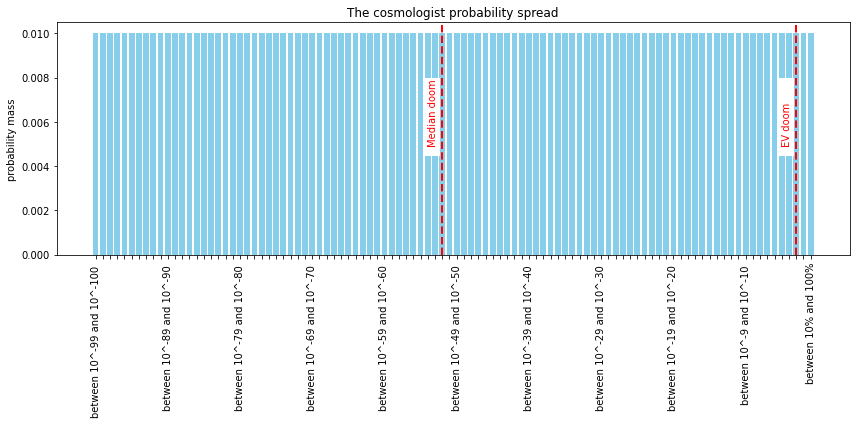
Cosmologist: Well, I’m a little uncomfortable with this, but I’ll give it a shot. I will tentatively say that the odds of doom are higher than 1 in a googol. But I don’t know the order of magnitude of the actual threat. To convey this:
I’ll give a 1% chance it’s between 10^-100 and 10^-99
A 1% chance it’s between 10^-99 and 10^-98
A 1% chance it’s between 10^-98 and 10^-97,
And so on, all the way up to a 1% chance it’s between 1 in 10 and 100%.
(Note that this is a bar chart, not the actual probability density function)
To summarise, I really have no idea of the true probability of such a difficult question. I mean, my 95% credence intervals spans 95 orders of magnitude!
The journalist thanks him for his time, and goes off to write the article. When it arrives a few days later, the cosmologist opens the paper to read the headline:
RENOWNED COSMOLOGIST PREDICTS 1 in 230 CHANCE OF SIMULATION SHUTDOWN
He is shocked to discover that his “prediction” has made shockwaves around the world. The “simulation shutdown research institute” has spread the prediction across the internet, and is using this headline to raise money.
Demanding answers, he immediately calls up the journalist.
Cosmologist: “I demand a retraction! I never said anything about 1 in 230 chance of shutdown, that’s ridiculously high!
Journalist: What you did give me was a distribution of probabilities. I merely did the extra step of converting this into a final probability. To get this, we calculated the expected value of doom over your distribution. You said there was a 1% chance of between 1 in 10^100 and 1 in 10^99, so the risk of doom from that scenario is ~1%* 10^-99, = 3*10^-101. From the next section, it was 1 in 10^99 and 1 in 10^98, so the risk from that slice is 3*10^-100, and so on.
Jumping to the end, we find a 1% slice that doom is between 10% and 100%, giving expected doom of around 0.3%. Adding them all up, we get your total chance of doom at around 0.43%, or 1 in 230. So you see, I was just summarizing your results.
Cosmologist: but “1 in 230” is on my distribution graph, and the graph shows it to be extremely unlikely for P(doom) to be that high. The median estimate was 10^-50. Theres a pretty big difference between 1 in 100000000000000000000000000000000000000000000000000 and 1 in 230.
Journalist: I have been tasked with assessing a threat. And sure, in over 95% of your scenarios, we are in a safe world where the threat of shutdown is miniscule to non-existent. I agree that we are probably in such a world. But what matters, when assessing the question “will we all die from shutdown”, are the worlds where shutdown is a substantial threat. You assigned a 1% chance to us living in Danger-world, where we stand a 10% to 100% chance of death. If you assigned a 1% chance to Danger-world, then why on earth would we say the odds of danger are 48 orders of magnitude lower than 1%?
Cosmologist: Hang on, my original answer to the question of “P(doom)” was “I don’t know at all”. I only put my distribution down because you forced me to quantify my ignorance. The distribution I made was as close to “I don’t know” as I could mathematically express. I went all the way down to 10^-100, a truly ridiculously small probability. And yet, with your method, suddenly “I don’t know” translates to “1 in 230”? As if I’m stating that I’m more likely to die in a simulation shutdown than in a plane crash?
Part 3: the dangers of single numbers:
I’m sure a lot of readers will be highly eager to bite the journalists bullet, and state that EV is just the correct way to calculate probability, and that the cosmologist really should claim a 1 in 230 chance of shutdown, if that was his probability distribution.
I don’t agree that it's that obvious. Let’s look at a scenario where the cosmologist is forced to make a decision based on this estimate:
The Hypnosis device scenario:
An inventor has secretly built a planet sized hypnosis device. If matrix lords exist and are watching us, this device is 100% guaranteed to hypnotize them into wanting to protect us, ensuring our safety from simulation shutoff forever.
The only small snag in the plan is that there is an unavoidable 1 in a thousand chance that the device will destroy the universe and kill all of humanity.
Somehow, the keys for the device end up in the hands of the humble cosmologist from earlier. A countdown warns that if he doesn’t deploy it within 5 minutes, the opportunity will be lost forever, and no-one will be able to build such a device again. Should he deploy the device?
The cosmologist has never seen any matrix lords, has no hard evidence that they exist, and has a median model estimate of the matrix lord threat at 10^-50. Nonetheless, under the EV model, he should deploy the device. Under EV estimates, the odds of doom will drop fivefold, from 1 in 230 to 1 in a thousand.
I can tell you, if I was the cosmologist, there’d be no way in hell I would push that button.
This type of scenario scenario is not as unlikely as it looks. Trade-offs exist between combatting different causes all the time.
For example, Eliezer Yudkowsky has suggested the world should be willing to bomb large AI datacentres as part of a global treaty, even if the nations holding them threaten nuclear retaliation. A good strategy if AI is super-dangerous, a potentially disastrous one if it isn’t.
Imagine if such an agreement is made, with every country except for America. The US decides to rebel, saying they are building a giant AI megacluster for the sole purpose of curing cancer and other illnesses. The global treaty nations threaten to airstrike silicon valley if they don't cease, but the US refuses to back down and threatens nuclear war.
Suppose the decision whether to launch such a strike falls to Charlie, who thinks there is a 99% chance all AI risk is bullshit, but has a 1% credence in the doomer argument that the megacluster would kill all humans. Should he pull the trigger and airstrike silicon valley, actively killing civilian software engineers and risking nuclear war, despite being 99% convinced that AI is not an actual threat? Assuming the risk of extinction from a nuclear exchange isn't that high, the EV view would say that he should.
I disagree. I think he'd be crazy to pull the trigger!
What I have a problem with here is that the EV view seems to be privileging the unknown.
Asteroid strikes are very real existential threats, and we have a lot of evidence about them. We can see them, we can study them, we can get fairly good estimates for the frequency of really deadly ones. We have conclusive proof that we don’t live in danger-world, because if we did humanity would not have had time to evolve. As a result, the odds of a dinosaur-extinction sized impact this century is something of the order of 1 in a million.
Now compare that to the cosmologists assessment of matrix lords. Absolutely zero hard evidence, no reason to believe it’s true. but under his assessment, the EV risk is 1 in 230. The reason is that he has no conclusive disproof of the danger-world hypothesis.
It seems to me that this strategy inherently rewards problems that are difficult to disprove or unfalsifiable. It feels like you can do the same analysis as the cosmologist for things like UFO’s, ghosts, psychic mind control, and get the answer that they are bigger risks than asteroid risks.
Conclusion
I decided to publish this in draft form because I don't have a solution and I am not fully confident in my claims. I think people have debated this "dealing with uncertainty" thing before, it looks like Dempster-Shafer theory is an attempt to address it? I would be interested to hear feedback on whether people think my post brings up a real problem, and if so, what the solution is.
I remain suspicious of single number P(doom) estimates.


I think the root of the problem in this paradox is that this isn't a very defensible humble/uniform prior, and if the cosmologist were to think it through more they could come up with one that gives a lower p(doom) (or at least, doesn't look much like the distribution stated initially).
So, I agree with this as a criticism of pop-Bayes in the sense that people will often come up with a quick uniform-prior-sounding explanation for why some unlikely event has a probability that is around 1%, but I think the problem here is that the prior is wrong[1] rather than failing to consider the whole distribution, seeing as a distribution over probabilities collapses to a single probability anyway.
Imo the deeper problem is how to generate the correct prior, which can be a problem due to "pop Bayes", but also remains when you try to do the actual Bayesian statistics.
Explanation of why I think this is quite an unnatural estimate in this case
Disclaimer: I too have no particular claim on being great at stats, so take this with a pinch of salt
The cosmologist is supposing a model where the universe as it exists is analogous to the result of a single Bernoulli trial, where the "yes" outcome is that the universe is a simulation that will be shut down. Writing this Bernoulli distribution as B(γ)[2], they are then claiming uncertainty over the value of γ. So far so uncontroversial.
They then propose to take the pdf over γ to be:
p(γ)={0if γ<10−100kγfor 10−100≤γ≤1(A)Where k is a normalisation constant. This is the distribution that results in the property that each OOM has an equal probability[3]. Questions about this:
Is this the appropriate non-informative prior?
The basis on which the cosmologist chooses this model is an appeal to a kind of "total uncertainty"/non-informative-prior style reasoning, but:
This results in a model where E(γ)=−1/ln(x)=1/100ln(10)≈1in230 in this case, so the expected probability is very sensitive to this lower bound parameter, which is a red flag for a model that is supposed to represent total uncertainty.
There is apparently a generally accepted way to generate non-informative-priors for parameters in statistical models, which is to use a Jeffreys prior. The Jeffreys prior[4] for the Bernoulli distribution is:
p(γ)=1√γ(1−γ)(B)This doesn't look much like equation (A) that the cosmologist proposed. There are parameters where the Jeffreys prior is ∝1x, such as the standard deviation in the normal distribution, but these tend to be scale parameters that can range from 0 to ∞. Using it for a probability does seem quite unnatural when you contrast it with these examples, because a probability has hard bounds at 0 and 1.
Is this a situation where it's appropriate to appeal to a non-informative prior anyway?
Using the recommended non-informative prior (B), we get that the expected probability is 0.5. Which makes sense for the class of problems concerned with something that either happens or doesn't, where we are totally uncertain about this.
I expect the cosmologist would take issue with this as well, and say "ok, I'm not that uncertain". Some reasons he would be right to take issue are:
The real problem the cosmologist has is uncertainty in how to incorporate the evidence of (2) into a probability (distribution). Clearly they think there is enough to the argument to not immediately reject it out of hand, or they would put it in the same category as the turtle-universe, but they are uncertain about how strong the argument actually is and therefore how much it should update their default-low prior.
...
I think this deeper problem gets related to the idea of non-informative priors in Bayesian statistics via a kind of linguistic collision.
Non-informative priors are about having a model which you have not yet updated based on evidence, so you are "maximally uncertain" about the parameters. In the case of having evidence only in the form of a clever argument, you might think "well I'm very uncertain about how to turn this into a probability, and the thing you do when you're very uncertain is use a non-informative prior". You might therefore come up with a model where the parameters have the kind of neat symmetry-based uncertainty that you tend to see in non-informative priors (as the cosmologist did in your example).
I think these cases are quite different though, arguably close to being opposites. In the second (the case of having evidence only in the form of a clever argument), the problem is not a lack of information, but that the information doesn't come in the form of observations of random variables. It's therefore hard to come up with a likelihood function based on this evidence, and so I don't have a good recommendation for what the cosmologist should say instead. But I think the original problem of how they end up with a 1 in 230 probability is due to a failed attempt to avoid this by appealing to an non-informative prior over order of magnitude.
There is also a meta problem where the prior will tend to be too high rather than too low, because probabilities can't go below zero, and this leads to people on average being overly spooked by low probability events
γ being the "true probability". I'm using γ rather than p because 1) in general parameters of probability distributions don't need to be probabilities themselves, e.g. the mean of a normal distribution, 2) γ is a random variable in this case, so talking about the probability of p taking a certain value could be confusing 3) it's what is used in the linked Wikipedia article on Jeffreys priors
∫10aakγdγ=kln(10)=constant
There is some controversy about whether this the right prior to use, but whatever the right one is it would give E(γ)=0.5
For some things you can make a mutual exclusivity + uncertainty argument for why the probability should be low. E.g. for the case of the universe riding on the back of the turtle you could consider all the other types of animals it could be riding on the back of, and point out that you have no particular reason to prefer a turtle. For the simulation argument and various other cases it's trickier because they might be consistent with lots of other things, but you can still appeal to Occam's razor and/or viewing this as an empirical fact about the universe
you are saying that if there are n possibilities and we have no evidence then probability is 1/n rather than 1/2. But for these topics there is an infinite set of discrete possibilities. Since the set is infinite it doesn't make sense to have uniform prior because there is no way for the probabilities to add up to 1.
I might also say "The 'true' P(heads) is either 0 or 1". If the coin comes up heads, the "'true' P(heads)" is 1, otherwise the "'true' P(heads)" is 0. Uncertainty exists in the map, not in the territory.
Okay, in in this specific context I can guess what you mean by the statement, but I think this is an inaccurate way to express yourself, and the previous “I have a 95% credence that the bias is between X and Y” is a more accurate way to express the same thing.
To explain, lets formalize things using probability theory. One way to formalize the above would be to use a random variable B which describes the bias of the coin, and then you could say P(X≤B≤Y)=0.95andP(heads|B=b)=bfor all b∈[0,1]. I think this would be a good way to formalize things. A wrong way to formalize things would be to say P(X≤P(heads)≤Y)=0.95. And people might think of the latter when you say “I have a 95% credence that the “true” P(heads) is between X and Y”. People might mistakenly think that "'true' P(heads)" is a real number, but what you actually mean is that it is a random variable.
So, can you have a probability of probabilities?
If you do things formally, I think you should avoid "probability of probabilities" statements. You can have a probability of events, but probabilities are real numbers, and in almost all useful formalizations, events are not in the domain of real numbers. Making sense of such a statement always requires some kind of interpretation (eg random variables that refer to biased coins, or other context), and I think it is better to avoid such statements. If sufficient context is provided, I can guess what you mean, but otherwise I cannot parse such statements meaningfully.
On a related note, a "median of probabilities" also does not make sense to me.
What about P(doom)?
It does make sense to model your uncertainty about doom by looking at different scenarios. I am not opposed to model P(doom) in more detail rather than just conveing a single number. If you have three scenarios, you can consider a random variable S with values in {1,2,3} which describes which scenario will happen. But in the end, the following formula is the correct way to calculate the probability of doom: P(doom)=P(doom|S=1)P(S=1)+P(doom|S=2)P(S=2)+P(doom|S=3)P(S=3).
Talking about a "median P(doom)" does not make sense in my opinion. Two people can have the same beliefs about the world, but if they model their beliefs with different but equivalent models, they can end up with different "median P(doom)" (assuming a certain imo naive calculation of that median).
What about the cosmologist's belief in simulation shutdown?
As you might guess by now, I side with the journalist here. If we were to formalize the expressed beliefs of the cosmologist's using different scenarios (as above in the AI xrisk example), then the resulting P(doom) would be what the journalist reports.
It is fine to say "I don't know" when asked for a probability estimate. But the beliefs of the cosmologist's look incoherent to me as soon as they enter the domain of probability theory.
I suspect it feels like a paradox because he gives way higher estimates for simulation shutdown than he actually believes, in particular the 1% slice where doom is between 10% and 100%.
I think in this context the natural way to interpret probabilities (or medians) of probabilities is as something like: "what would I think the probability was if I knew a lot more about the situation and got to think about it a lot more, but wasn't literally omniscient". Of course that isn't fully defined (since it's not specified exactly how much more they get to know), but I think it's approximately meaningful, and can capture something quite useful/important about credal resilience.
Relatedly, I think the journalist's presentation is misleading. I think it makes it sound like there's something like an objective 1-in-230 chance of catastrophe. I think a more accurate presentation would be "expert thinks there's a 1% chance we live in a world with a high risk". This changes the appropriate policy implications: if taken at face value they both suggest there's something important to do, but in the latter case the action is less like "work out what to do about simulation shutdown" and more like "start a serious research programme to work out how likely it is we're in the fraction of worlds that was offhand labelled as 1%".
(I also think that you may be right that the cosmologist didn't really believe their numbers. I think that issue alone would be enough reason to be suspicious of the journalist's approach. They might reasonably suspect that such off-the-cuff answers might not withstand scrutiny, so it seems bad to report them in a way that could sound like considered expert opinion.)
Hi titotal,
I think it makes sense to assess the annual risk of simulation shutdown based on the mean annual probability of simulation shutdown. However, I also believe the risk of simulation shutdown is much lower than the one guessed by the humble cosmologist.
The mean of a loguniform distribution ranging from a to 1 is -1/ln(a). If a = 10^-100, the risk is 0.434 % (= -1/ln(10^-100)). However, I assume there is no reason to set the minimum risk to 10^-100, so the cosmologist may actually have been overconfident. Since there is no obvious natural lower bound for the risk, because more or less by definition we do not have evidence about the simulators, I guess the lower bound can be arbitrarily close to 0. In this case, the mean of the loguniform distribution goes to 0 (= -1/(ln(0))), so it looks like the humblest view corresponds to 0 risk of simulation shutdown.
In addition, the probability of surviving an annual risk of simulation shutdown of 0.434 % (= 10^-5.44) over the estimated age of the universe of 13.8 billion years is only 10^-75,072,000,000 (= (10^-5.44)^(13.8*10^9)), which is basically 0. So the universe would have needed to be super super lucky in order to have survived for so long with such high risk. One can try to counter this argument saying there are selection effects. However, it would be super strange to have an annual risk of simulation shutdown of 0.434 % without any partial shutdowns, given that tail risk usually follows something like a power law[1] without severe jumps in severity.
Although I think tail risk often decays faster than suggested by a power law.
Executive summary: Bayesian probability distributions, rather than single point estimates, should be used when reasoning about highly uncertain risks like existential threats from AI, but this approach has some counterintuitive and potentially problematic implications.
Key points:
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.