This post is part of a living literature review series of societal collapse. You can find the most recent version here.
The first post of this living literature review gave a summary of the field of collapse studies. One thing that post makes clear is that we need better models of societal dynamics. This post explores the state of societal dynamics modeling.
Overview of different modeling approaches
One helpful work about societal dynamic modelling is a literature review by Sabin Roman, which I will use here as the basis to give a first overview (Roman, 2023) (1).
One thing that societal collapse research has shown is that we cannot attribute collapse to a single cause. However, we might track it back to a single process. Roman proposes here that to capture the complexities of collapse, we have to think in the form of feedback mechanisms. This means to understand collapse, we have to think in and model multi-causal relationships between a variety of societal variables. To give a more concrete example of such a feedback process, look at the self-reinforcing mechanism of famines, explained in an earlier post:
“
- A society that experiences a substantial loss of population will inevitably see a decline in its capacity to both produce and trade food resources.
- Reduced food production and trade result in a decreased availability of food within the society.
- The scarcity of food leads to increased instances of famine, exacerbating the prevalence of deaths and health-related issues, thus initiating the subsequent iteration of the cycle.
“
These feedback processes are an especially valuable tool if you want to do some quantitative modeling and Roman lays out the kinds of models that have been used to model societal collapse with feedback processes. Roman mainly differentiates between the way the models are set-up (agent based models vs. world models) and the fields they draw inspiration from (economic based models vs. ecologically inspired models).
Agent-based models vs. integrated world models
This is the difference between models that focus on the individuals and their interactions and models which are more concerned with modeling more abstract processes.
You can imagine agent-based models as a collection of simulated and very simplified individuals. They interact with each other on every time step of the simulation in the ways that the model allows. The idea is that this interaction between the individuals will produce an emergent pattern of behavior, which helps us understand social dynamics.
Integrated world models on the other hand don’t model the individuals, but instead try to understand how societal processes can be expressed in equations directly. They usually consist of a variety of variables which are coupled with each other. For instance, you could express the self-reinforcing mechanism of famines as equations and then let the model run with a variety of different input parameters, to see how this changes the feedback.
If we modeled the famine feedback cycle using an agent-based approach, our focus would likely be on the decision-making processes of individuals confronted with food scarcity. Each agent, driven by the need to collect enough food, would engage in interactions with other agents and factors such as food sources. This simulation would unfold over multiple time steps, with agents iteratively interacting. At the simulation’s conclusion, we would look at the state of all agents to determine the outcomes of their interactions. In the context of a famine scenario, this might show a segment of agents starving due to an inability to locate food, while others faring better by successfully securing enough food sources.
If we modeled the famine feedback cycle with a world model, we might instead focus overarching variables such as population, overall food reserves, and additional stressors like disease. Here, feedback mechanisms, implemented through differential equations, would establish connections between these variables. For instance, we might define that a higher population decreases food resources and that increased disease incidence leads to a population decline. Analogous to the agent-based model, this model would progress through successive time steps, with the differential equations influencing variable values. At the simulation’s end, we can examine the variables, such as whether the population increased or decreased for example.
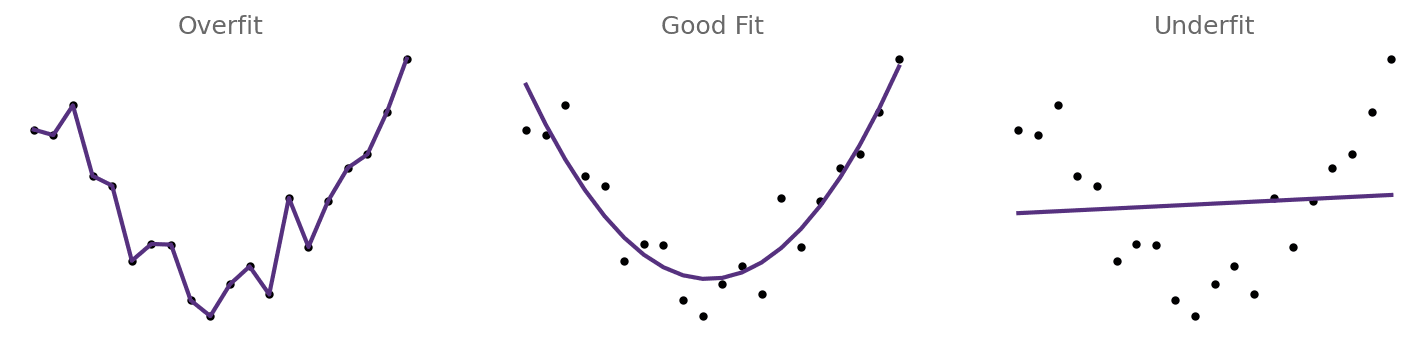
Both kinds of models run into the problem that it is very difficult to find the right number of parameters, as well as their correct values, both for the behavior of the individuals in the agent-based modeling, but also for the feedback mechanisms in world models. You need enough parameters to be able to accurately model your data, but the more parameters you have, the more data you need to meaningfully constrain their values. This means you have a trade-off between underfitting and overfitting (Figure 1), which is hard to get right.
Figure 1: Example of over and underfitting data.
Economic based models vs. ecologically inspired models
Models also differ in drawing inspiration from economics and ecology. These models don’t necessarily differ in the tools they use, but in the assumption behind them. Economic based models usually assume rational, utility-maximizing agents. This is often expressed as a utility function. These models typically try to fit the data with models that assume humans are completely rational agents. According to Roman this has not worked out well. While the economic based models have increased in complexity over time, they still struggle to be in line with the archeological data we have.
Ecologically inspired models on the other hand try to use collapse-like mechanisms we find in nature to show how societies rise and fall. These are then calibrated on empirical archeological data. An example of this is the Roman Empire Model in the next section. According to Roman, these ecological processes seem to fit the rise and fall of civilizations better.
Examples of models
In the following I want to highlight two models. A system dynamics model by Roman & Palmer (2019), which simulates the complete life cycle of the Roman Empire and the classic Limit to Growth model (Herrington, 2021). I focus on these two models as Roman and Palmer (2019) can be seen as a very recent approach to collapse modeling, while the limits to growth model is the most studied collapse model we have.
Quantifying the collapse of the Roman Empire
We’ll begin with the Roman and Palmer model. With this model Roman and Palmer want to implement the feedback mechanisms they think are important for the overall trajectory of the Roman Empire. To find out which ones are most important, they review the literature around the Roman Empire and settle on army size, overall territories, territory changes and coinage. The idea here is that army size controls how much territory you can gain and hold, the territory you have influences your coinage and the coinage influences how much soldiers you can pay. Roman and Palmer use a world model and represent each of these feedback mechanisms via connected ordinary differential equations.
The model itself has 10 parameters which govern those equations (e.g. the net growth rate of the silver reserves). To simplify, think of each parameter as a knob adjusting different parts of the model. The number of parameters are based on the number of stocks in the model, which means there is a parameter for each one-way connection between variables, including self-loops. They decide on a plausible range for those parameters and fine tune them by hand to get a good visual fit of their model outputs and observed historical data.
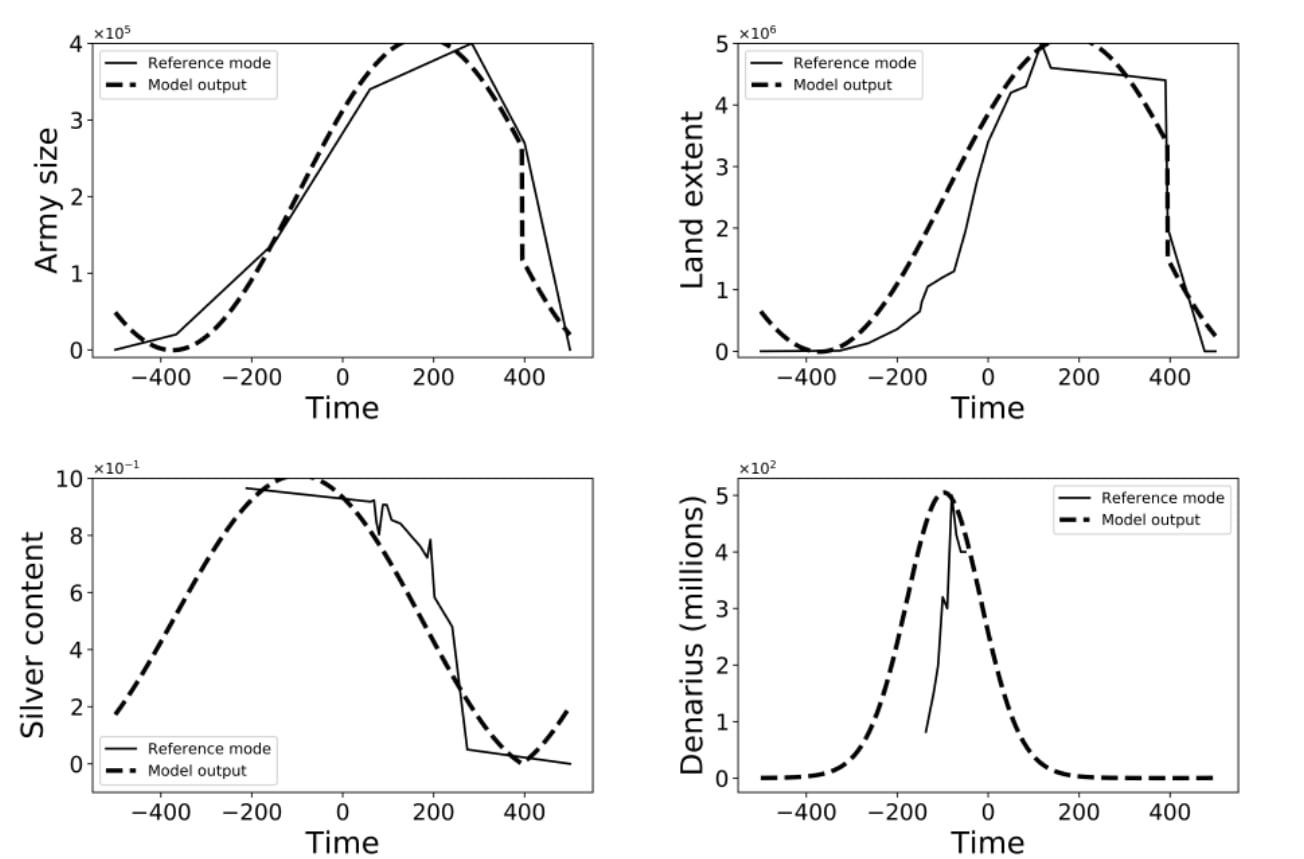
Figure 2: Comparison of simulated (dotted line) and historical data (solid line) for the Roman Empire model (Roman & Palmer, 2019)
As you can see in the results of this model (Figure 2) the model is able to roughly capture the overall trends, but struggles with the finer details and especially the amount of money (denarius - bottom right figure). Still, this is to be expected as the data used is sparse and also often based on proxies and estimations itself, further introducing uncertainty. One downside of the model is that it is custom made for the Roman Empire. So, even if it helps us understand why and how the Roman Empire collapsed, it will be very difficult to extrapolate any of those findings to modern society or other civilizations in general.
Limits to Growth
The original Limits to Growth model was published 1972. It had the aim to understand where the trajectories about things like population, resource use and climate change would lead us in the future. To do so they created the so-called World3 model. This model is very much on the side of an ecologically inspired integrated world model when we use the definitions above. It tries to capture the dynamics of many aspects of our global civilization and how they interact. It tries to simulate the future, by extrapolating the trends of 1972 in a variety of scenarios. These scenarios differ in their assumption of how many resources exist in the world and how humanity reacts to the challenges before us.
In contrast to almost all other collapse models I found, this one is not concerned not with some past society, but with the one we live in right now. This obviously introduces the problem that we cannot easily validate the model, as we don’t know what will happen in the future. However, the model was published more than four decades ago, so much of the predicted future has already happened and we can check how it held up. This is exactly what Herrington (2021) did.
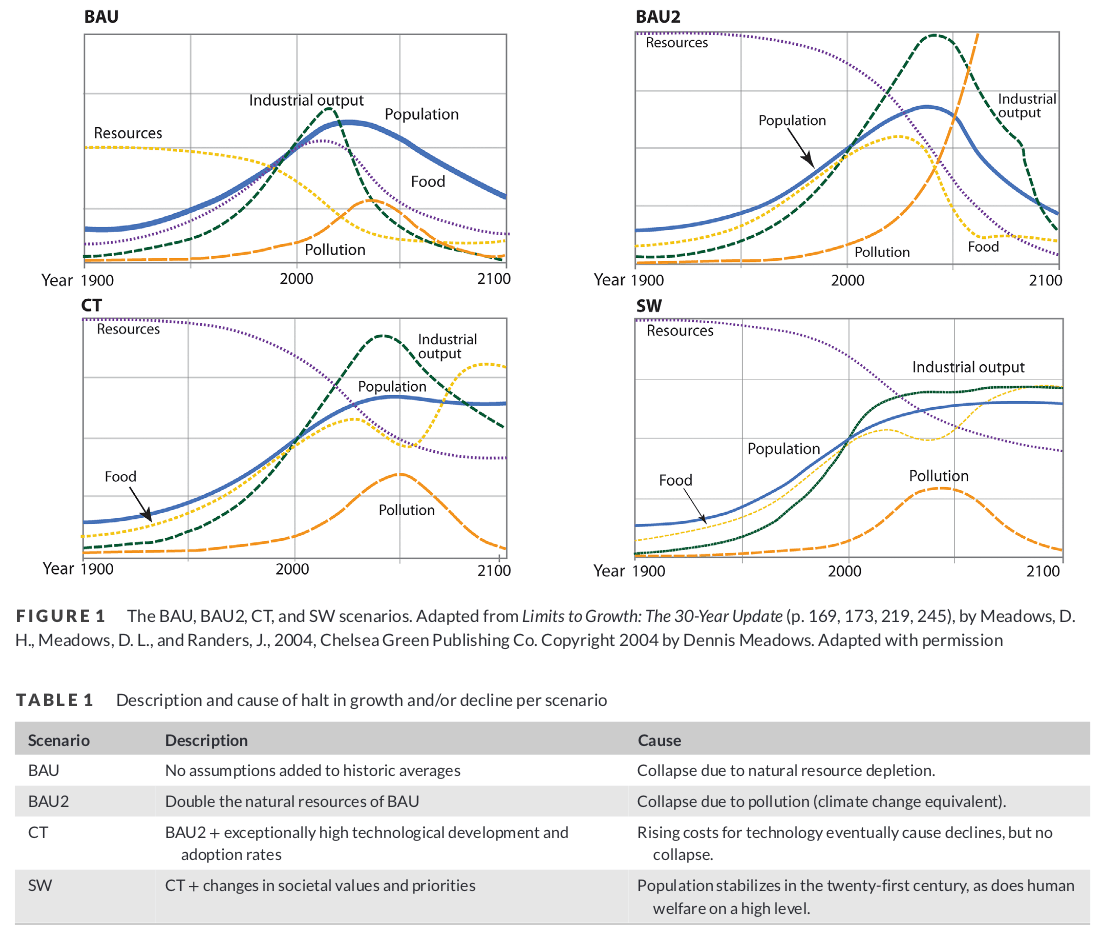
In her analysis she compared the outputs (Figure 3) of the limits to growth model with the actual data we have right now. She finds the model was relatively accurate in tracking our path so far. However, this comes with a big caveat. The model does not predict much differences between the different scenarios until 2020-2030. Therefore, we only know that the model has not been falsified so far, but it is still unclear what the path is we are currently on.
Figure 3: Scenarios and trends of the Limits to Growth model.
How helpful are those models?
It seems to me that there is much work to be done on social collapse modeling. A major challenge is developing models that are transferable between societies. Right now many models are custom made for a single society. While those are easier to construct and can give important insights they make it hard to generalize their findings. Two other things jumped out to me during this review:
- We need more and better data. History has been a very qualitative science for much of its history. Only recently big databases like SESHAT (Turchin et al., 2019) (2) started to be constructed, which contain standardized data for a variety of civilizations over a long time period. However, SESHAT cuts off at the industrial revolution, so it gets quite difficult to compare societies across this gap. Having a SESHAT like database which includes societies after the industrial revolution would be very valuable to validate our models.
- Societal collapse models could learn from other fields when it comes to building, calibrating and validating models. Right now models in this field seem very custom made, with everyone developing their own tools and ideas for things like calibration. However, other fields have been building models of similar structure and complexity for decades by now. An example I am familiar with is hydrology. There, so called lumped models are also trying to express natural processes at an aggregated level as a collection of connected differential equations. That field has made some insights that might be interesting to collapse modelers:
- Automatic model calibration: Calibrating models by hand has been deprecated in hydrology, as it often allows researchers to let their biases influence the models results and also does not give any real benefits. An example of an automatic calibration toolkit would be SPOTPY (Houska et al., 2015).
- Model building toolkits: The exact structure of your model is often grounded more in a researcher’s bias, than in the real world. Therefore, in hydrology the trend has shifted to model building toolkits. Those allow the easy construction of different model structures, so you can also explore how differences in the structure of your model shape your results. An example here is the catchment modeling framework (CMF) (Kraft et al., 2011). This works by creating modular components for the model, such as providing various implementations of the same process, for instance simulating infiltration of water into the soil. These components can be easily bolted together to allow building a new model quickly. Modifying specific blocks enables the isolation of changes’ effects, which in turn makes it easier to understand the model’s functioning and compare it to other models built using the same toolkit.
- Finding meaningful parameter values is very hard: When researchers construct models, they often think that the processes they implement and the parameter values they choose at least roughly map to a real world process. However, this likely is often not the case. This only becomes obvious if your model has several outputs, which can be compared to real world data. Changes in parameters which allegedly represent real world processes often lead to making one output of the model better, in exchange for another output getting worse. How this plays out is described for example in Houska et al. (2021).
- Model complexity: Having a complex model does not necessarily mean that you have a better model, especially if you do not have the data to meaningfully constrain its parameters. Complex models have other drawbacks as well, like long run times for instance. This makes it much harder to learn and iterate. This is also nicely summarized in a quote by Donella Meadows: “Models can easily become so complex that they are impenetrable, unexaminable, and virtually unalterable.” This means we always have to be aware of the balancing act of putting all the necessary parts in our model, while not overloading it with more than our data can constrain.
All this does not mean that the models we have are useless. They give us insights which could not be obtained otherwise. And when we compare them with models from the natural sciences we have to be careful, as those models have had decades or even hundreds of years to be refined, while societal dynamics modeling is still in its early stages. I think that if we spend more resources on this field, I would expect a quick improvement, as many low hanging fruits remain unpicked due to a lack of resources and time. To illustrate this, I am only aware of a handful of societal dynamics models, while in hydrology, a recent paper implemented 47 of the most popular hydrological models into a single framework, to allow easier comparisons across models (Trotter et al., 2022). Given the state and resources in societal dynamics modeling, it seems unlikely to me that such a project would be possible there anytime soon. Once this field has become more established, I would expect that many of the problems highlighted here will become less important over time.
Endnotes
(1) This is a chapter from the book “The Era of Global Risk” (Beard et al., 2023), which gives an overview of the current state of existential risk studies and related topics.
(2) SESHAT is discussed in more detail in this earlier post.
References
Beard, S. J., Rees, M., Richards, C., & Rios Rojas, C. (2023). The Era of Global Risk: An Introduction to Existential Risk Studies. Open Book Publishers. https://doi.org/10.11647/obp.0336
Herrington, G. (2021). Update to limits to growth: Comparing the World3 model with empirical data. Journal of Industrial Ecology, 25(3), 614–626. https://doi.org/10.1111/jiec.13084
Houska, T., Kraft, P., Chamorro-Chavez, A., & Breuer, L. (2015). SPOTting Model Parameters Using a Ready-Made Python Package. PLOS ONE, 10(12), e0145180. https://doi.org/10.1371/journal.pone.0145180
Houska, T., Kraft, P., Jehn, F., Bestian, K., Kraus, D., & Breuer, L. (2021). Detection of hidden model errors by combining single and multi-criteria calibration. Science of The Total Environment, 777, 146218. https://doi.org/10.1016/j.scitotenv.2021.146218
Kraft, P., Vaché, K. B., Frede, H.-G., & Breuer, L. (2011). CMF: A Hydrological Programming Language Extension For Integrated Catchment Models. Environmental Modelling & Software, 26(6), 828–830. https://doi.org/10.1016/j.envsoft.2010.12.009
Roman, S. (2023). 2. Theories and Models: Understanding and Predicting Societal Collapse. 27–54. https://doi.org/10.11647/obp.0336.02
Roman, S., & Palmer, E. (2019). The Growth and Decline of the Western Roman Empire: Quantifying the Dynamics of Army Size, Territory, and Coinage. Cliodynamics, 10(2). https://doi.org/10.21237/C7clio10243683
Trotter, L., Knoben, W. J. M., Fowler, K. J. A., Saft, M., & Peel, M. C. (2022). Modular Assessment of Rainfall–Runoff Models Toolbox (MARRMoT) v2.1: An object-oriented implementation of 47 established hydrological models for improved speed and readability. Geoscientific Model Development, 15(16), 6359–6369. https://doi.org/10.5194/gmd-15-6359-2022
Turchin, P., Whitehouse, H., Francois, P., Hoyer, D., Alves, A., Baines, J., Baker, D., Bartkowiak, M., Bates, J., Bennett, J., Bidmead, J., Bol, P., Ceccarelli, A., Christakis, K., Christian, D., Covey, A., De Angelis, F., Earle, T., Edwards, N., & Xie, L. (2019). An Introduction to Seshat: Global History Databank. Journal of Cognitive Historiography, 5. https://doi.org/10.1558/jch.39395

Nice post!
I think it would be helpful to see an overlay of our actual trajectory. Though the absolute values of the models are not that different for the period 2000 to 2020, the slopes are quite different. I think there was a paper analyzing the fits including the slopes. The increase of production of food since the year 2000 has been much larger than any of the models predicted. Also, I think the increase in industrial capacity is higher than any of these models. Interestingly, some people interpret this as us overshooting farther, so then we will fall more dramatically. But because we generally have not seen reduction in slopes, I don't really see evidence for this, so I think that the optimistic interpretation is more likely to be right, basically that we have innovated around limits to growth so far.
Thanks David. I think the paper you are referring to might be the one I cited. At least Herrington also looked at the rate of change as well (Table 2). There you can see that the current trajectory and rate of change is most similar to the CT and the BAU2 scenario. CT being a scenario like you described (we innovated ourselves out of limits to growth), while BAU2 being a scenario where we are still on a collapse trajectory, but the resources of Earth are 2x of the default limits to growth scenario. Therefore, I would argue that we still can't tell if we just had more resources on Earth than originally estimated or if we solved our problem with innovation. But if you have another paper that discusses this as well, I'd be happy to read it.