Summary
- I make three arguments against standard difference-making risk aversion that I find compelling as a consequentialist, despite my substantial sympathy for something like difference-making risk aversion:
- It privileges a default option, literally as or like an act-omission distinction, or is otherwise unmotivated (more).
- It may lead generally to inaction or otherwise favouring the default option, due to multitudes of backfire risks and butterfly effects (more).
- It can count against you persuading others to take actions that are less risky from their perspectives, and when the default option is a status quo option, it favours the status quo (more).
- Some of these arguments also apply to difference-making ambiguity aversion.
- I describe multiple versions of or modifications of difference-making views that don't have these problems. Some can also be combined. They are:
- use accounts that treat downsides and upsides relative to the fixed default option more symmetrically (more),
- statewise sorting, so that we aren’t sensitive to how outcome distributions correspond statewise (more), and
- not privileging inaction as the default option to make comparisons with respect to, but potentially treating every option this way (more).
Acknowledgements
Thanks to Derek Shiller, Silvester Kollin and Anthony DiGiovanni for helpful feedback. All errors are my own.
Background
For further background on and discussion of difference-making risk aversion, see Clatterbuck, 2024 and Greaves et al., 2022. I only illustrate briefly here.
If you're risk averse with respect to money, it's better to have a $50 with certainty than a 50% chance of $0 and a 50% chance of $100, even though your expected amount of money is $50 either way.
Suppose we have some quantity for which it is better that its value be higher, like money or total welfare. In economics and according to expected utility theory, this quantity has some utility, captured by an increasing utility function, , of the quantity, and we would pick an option with maximum expected utility, .
On the standard economic and expected utility theory account of risk aversion, is increasing and concave, i.e. the quantity has diminishing marginal utility.[1] Examples of such functions are for , and .
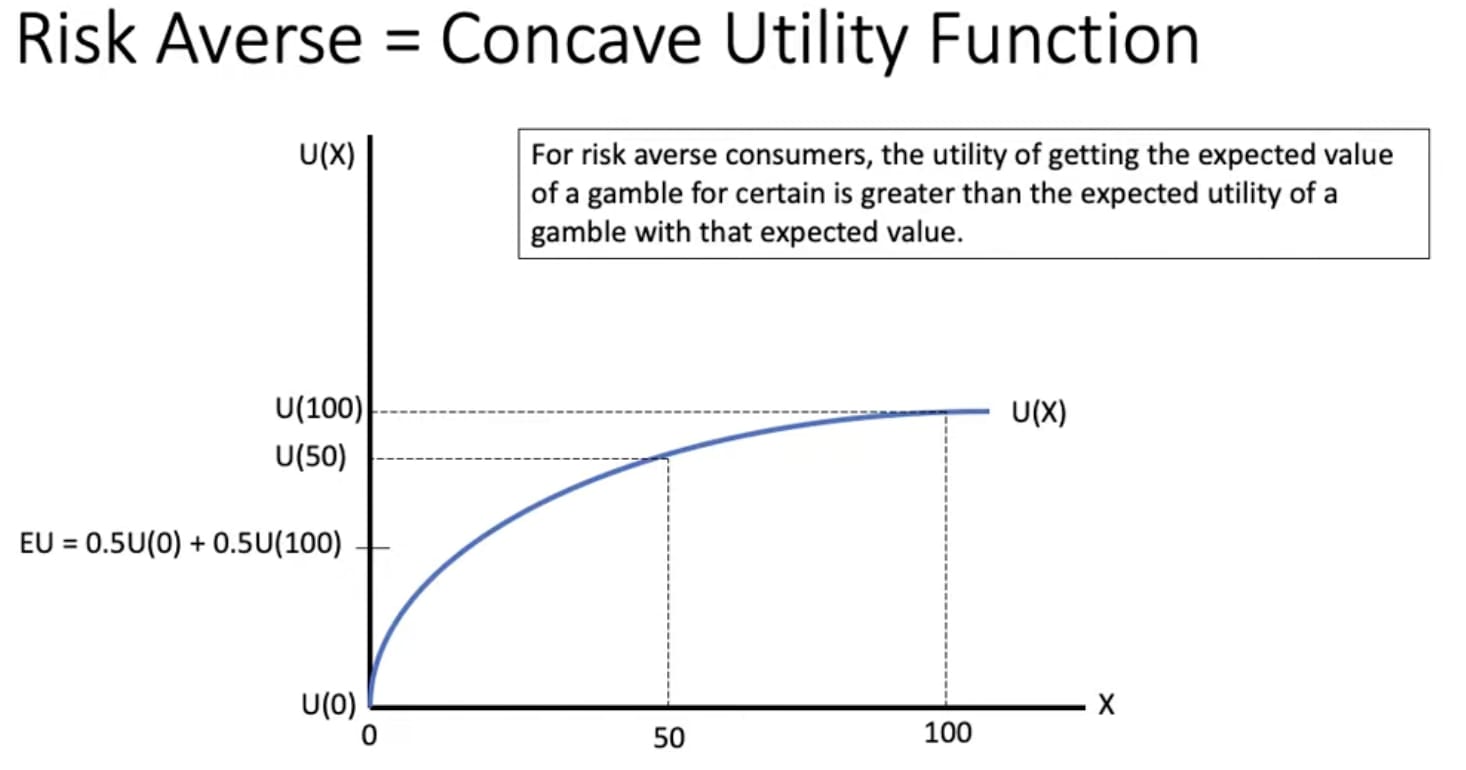
With diminishing marginal utility, the expected utility of the 50-50 gamble for $100 is lower than the (expected) utility of $50 with certainty:
On the other hand, the standard account of difference-making risk aversion is, for a given choice situation, to fix some default option , e.g. doing nothing or business-as-usual, and compare options to it, and be risk averse with respect to the difference in outcome "value" between and . I’ll illustrate.
We again fix some function that is increasing and concave to capture risk aversion. Then, a specific version of difference-making risk averse falling under the standard account would be to pick the option that maximizes the following quantity:
where the expected value is taken over the probability distributions over outcomes and . Taking itself will sometimes maximize this expected value among available options.
Against standard difference-making
I think the standard version of difference-making risk aversion, in which you hold some default option constant and compare every other to it, is very unattractive (to me) under consequentialism for three reasons.
Privileging a "default option" is incompatible with consequentialism or unmotivated
Picking one option to compare to privileges it, and if that option is an omission or "doing nothing", this makes some kind of an act-omission distinction and tends to favour omissions, all else equal. Consequentialists typically reject act-omission distinctions (Woollard, 2021). If we are concerned only with the (actual or predicted) consequences of the options available to us, inaction is not fundamentally special and worth singling out at a foundational level, whether or not it’s special in practice. Controlling for the consequences of an option, whether it is identified as an action or inaction should have no bearing on how choiceworthy it is, because only the consequences matter.
Privileging the status quo or business-as-usual or any other particular option in a given choice situation from the outset in a fundamental way also seems unmotivated morally for an impartial consequentialist.
A related objection is that difference-making is partly egoistic and not very impartial at all (Greaves et al., 2022). Why should you care about the difference you make relative to some conveniently selected option, rather than just what’s best, or is stochastically dominant?[2] Indeed, I object to many non-consequentialist views similarly: privileging the avoidance of committing harm, even if committing that harm would lead to better overall consequences, seems to me overly concerned with my own position. Perhaps uncharitably, it seems more like trying to keep my hands clean than impartially respecting the subjective interests at stake. The same seems to apply to privileging inaction for difference-making risk aversion.
Of course, privileging the avoidance of committing harm may lead to better consequences in practice. It could even be that someone who isn’t difference-making risk averse would do better on their original view by becoming difference-making risk averse, independently of the plausibility of difference-making risk aversion. This could be because many consequentialists may fail to appreciate the instrumental value of cooperation and respecting social norms or the particular downsides for other consequentialists in committing harm, and then we end up with some of us committing financial fraud on one of the largest scales in recent history (O’Connell, 2024), and potentially hurting the efforts of effective altruism community.
But this is a practical argument for difference-making risk aversion, and doesn’t seem very compelling to me as an argument that it’s actually morally correct.[3] There could be better ways to mitigate such risks that don’t involve abandoning a view that seems more likely correct.
Potentially severely favours inaction or the default
Difference-making risk aversion plausibly leads to generally favouring inaction or the default, when you factor in backfire risks, including unknown backfire risks and backfiring butterfly effects.
I suspect almost any intervention EAs support has important and predictable backfire risks. Many are specific to the intervention or cause area. A potentially common one could be what you support funging with risky work.
Even if an act you're considering and the default have the same chance of causing a tornado from butterfly effects, as long as the outcomes with the extra tornado(es) don't correspond statewise between the two acts and assuming tornadoes are harmful, then this will count against your act under difference-making risk aversion.
To illustrate mathematically, consider two options, for default, and , with states and , each occurring with probability 50%, and the following corresponding values:
| Option / state | a | b |
| D | 0 (tornado) | 1 (no tornado) |
| A | 1 (no tornado) | 0 (tornado) |
Under difference-making risk aversion, we should prefer , even though the two options have identical payoff distributions. Even increasing the value of by a small enough amount, we should still prefer , even though would then stochastically dominate it and have higher direct expected value.
Difference-making risk aversion — compared to risk neutrality — effectively gives less weight to upsides of an action over the worst cases of inaction and more weight to downsides of action under the best cases of inaction.
And including differences between far future impacts or impacts on wild invertebrates could count a lot against many acts, because these impacts can be very large in scale, potentially much larger than the main impacts we’re assessing, in the extreme cases. Evidential symmetry doesn't help if the values of outcomes don't correspond statewise.
Disfavours changing plans
There’s reason to believe diet change, including vegan and reducetarian advocacy and support for animal product substitutes, has huge effects on wild animals, especially wild invertebrates, by increasing or decreasing their populations (e.g. Tomasik, 2019). Depending on your views, this could go in either direction, possibly extremely good, e.g. dramatically increasing the number of good lives and possibly extremely bad, dramatically increasing the number of bad lives.[4]
If the overall effects of diet change are too risky from your position, because of potentially huge backfire effects on wild animals, but the potential upside for wild animals are also huge, then convincing Open Phil to do less diet change (and more of something else) can backfire for you by losing this huge potential upside. The lost huge potential upside for wild animals from Open Phil’s perspective becomes a huge potential downside relative to inaction from your perspective.
In general, if someone is doing something risky with both huge potential upsides and huge potential downsides from their position, it doesn’t follow that getting them to do something less risky from their position instead is actually good from your position. When considering shifting their risky work to something less risky, the huge potential upsides of their risky work become huge potential downsides from your position.
Similarly, if my current plan is my default option to compare to — rather than doing nothing or because sticking to it is doing nothing —, then I will tend to favour that plan. For example, I may have already decided on what charities to give to and will do that by default. Or I may have even set up recurring donations that will go on without my intervention. Considering options further and intervening to change my plan is an action, not inaction, and is disfavoured. This looks like status quo bias to me.
Difference-making views that can avoid these problems
There are a few difference-making views that can avoid the problems above. They seem more attractive to me. I outline these as modifications of the view I presented above, and some of them can be combined.
More symmetry
Measure the difference both ways and take the difference
When the default option is , we measured the value of an option relative to it as , e.g. . Instead, we could also measure the value of the difference treating as the default option, , and take the difference:
and pick whichever option has the highest such value.
In doing so, we consider both the risk of A relative to and the risk of relative to A and treat them symmetrically.
Of course, we still privilege , because every comparison involves , but we can combine this with an approach from Not privileging inaction if we wanted to avoid this.
A sigmoidal rather than concave function
Rather than risk aversion and a concave function u, we should instead give less than proportional weight to both upsides and downsides. We can use a utility function of the difference we make such that is increasing, ( is an odd function), and u is concave above and to the right of 0 (and possibly bounded above and below), but convex below 0 and to the left of 0. The arctan function, a sigmoid function, is a good example:
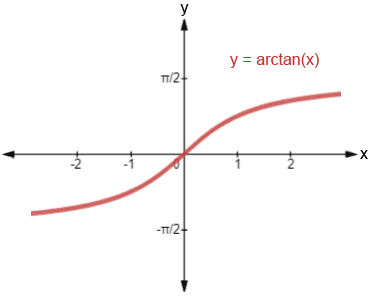
This approach does not privilege the default option at all in pairwise comparisons with the default option. It is less (or not) fanatical about backfire risks, so doesn't lead to paralysis or bias against changing plans.
It’s also less fanatical in general, and so more likely to support neartermist interventions and disproportionate priority for beings more likely to be sentient, compared to risk neutral views and most other attitudes towards risk.
Bounded utility functions, including sigmoid functions, also seem more rational, i.e. less prone to selecting dominated strategies (St. Jules, 2023).
However, like in the previous subsection, the default option is still privileged because it's used in every comparison.
Statewise sorting
As before, consider two options, for default, and , with states and , each occurring with probability 50%, and the following corresponding values:
| Option / state | a | b |
| D | 0 (tornado) | 1 (no tornado) |
| A | 1 (no tornado) | 0 (tornado) |
Under difference-making risk aversion, we should prefer , even though the two options have identical payoff distributions. Even increasing the value of by a small enough amount, we should still prefer , even though would then stochastically dominate it and have higher direct expected value.
Instead, we can relabel and sort their states in increasing order of value, in this case with states and with probability 50% each:
| Option / state | c | d |
| D’ | 0 (tornado) | 1 (no tornado) |
| A’ | 0 (tornado) | 1 (no tornado) |
If we apply our difference-making criterion to and instead of directly to and , we would be indifferent between and , and we can lift that indifference to and . If had instead stochastically dominated , then applying our difference-making criterion to and and lifting that to and would favour . That is, we choose to maximize our measure between and , with as the default. For example, with concave, reflecting diminishing marginal utility:
I will call the approach statewise sorting. I outline it more generally and technically in the following footnote.[5]
This approach will rule out strictly stochastically dominated options. By doing so, it will be sensitive to the welfare of unaffected beings, which may seem odd and counterintuitive, and could support longtermism (Tarsney, 2020, Tarsney, 2023).
To address the dependence on unaffected beings, we could just omit them from consideration in the state’s value before relabeling and sorting the states. After all, we make no difference to them, and we're interested in difference-making here. However, this would no longer respect stochastic dominance with respect to outcomes.
Furthermore, statewise sorting also gives up some of the appeal of difference-making, which we may take to be inherently statewise. We might think the differences we’d make just are statewise differences, so they deserve special treatment. And we might not care about stochastic dominance, because it doesn’t leave us worse off statewise. Only statewise dominance leaves us worse off statewise, and standard difference-making already respects this.
Statewise sorting also still privileges the default option on its own, but we can avoid doing so by combining it with approaches that don’t privilege inaction, described next. But doing so will typically mean allowing violations of the independence of irrelevant alternatives.
Not privileging inaction
Use the random option as the default
Suppose we have options available to us for consideration, . Let be the option which is to pick option with probability . We’ll call the random option. Then, we’ll make our comparisons treating as the “default option”, , comparing measures like and . Now, no particular option available to us seems especially privileged or favoured.[6]
Using the random option as the default to compare to can also be motivated independently: if we didn’t yet know any facts about the options available to us other than their number, then no matter which rule we use to pick an option, we should believe we’ll pick each option with probability .[7] The random option is the option we get under ignorance. It is in fact what we would actually do by default under full ignorance about which option is which, unable to even identify the “do nothing” option better than chance.
However, this may be a fairly unusual and contrived hypothetical: we’re practically never in a position of knowing nothing at all about our options, including which is which and especially which is the “do nothing” (or “status quo”) option. The “do nothing” option is (almost?) always obvious to us.
Furthermore, the random option depends on the available options, so whether beats could depend on whether or not an option is also available. Some find this kind of thing counterintuitive, and instead insist on the independence of irrelevant alternatives (IIA): whether beats should never depend on whether or not another option is also available. This view violates IIA.
That being said, I do not find all violations of IIA counterintuitive, as long as I am sufficiently sympathetic to the reason for the violation. In this case, a reason we can offer for the violation of IIA is that what we’d do with no knowledge about which option is which, i.e. the random option, depends on what options are available to us. That has some intuitive appeal to me. On the other hand, the intuitive appeal seems limited, given how unnatural the hypothetical seems to me. And it’s not clear why I should compare to what I’d do with no knowledge about which option is which. It just seems better to me than singling out inaction as a consequentialist.
And violating IIA can be avoided in practice, if and because we use the “do nothing” option as the default, and exactly one such option is practically always available to us.
There are some other concerns related to individuating and counting options, but these seem addressable in principle, although probably using vague standards.[8][9]
Use the expected value-maximizing or -minimizing option or outcome as the default
Instead of the “do nothing”, “status quo” or random option as the default, we could let the default option be, among those available to us, the one that maximizes expected value without or ignoring difference-making risk aversion, . Or, the expected value-minimizing option without difference-making risk aversion, . Or just the best outcome, , or worst outcome, , among those available to us.[10] So, or , respectively. Or, we could use the best or worst outcome among all conceivable outcomes, instead of just among those available to us.
When comparing to the maximizing option or best outcome as the default, we might think of the differences relative to it like a weighted net shortfall.
When comparing to the minimizing option or worst outcome as the default, we might think of the differences relative to it as how much better overall we can do than the worst.
We could also combine these, e.g. by adding , and ranking each option based on this associated value.
These approaches too will violate the independence of irrelevant alternatives as long as the (or an) option or outcome chosen as default is selected from those available to us, but they don’t seem (as) sensitive to how options are individuated. And they do still privilege an option (or outcome).
Use every option as the default
Another approach is to compare each option to every other option with a difference-making risk averse function, effectively treating each option as the default to compare to in turn. Then, use some rule to select an option that takes into account all of these comparisons, without specifically privileging any option at the start. There are multiple ways to do so, which I describe below.
Aggregating
One specific approach would be to let each option A act as the default, take the measures of difference-making risk aversion of every other option relative to that option as the default, , and sum them over all options to get :
Then we pick whichever option A has the lowest . This is the option for which the others are risk averse worst in aggregate relative to it.
Or, we vary the default option and sum over all options to get :
and then pick whichever option B has the highest . This is the option which is the risk averse best in aggregate relative to all others.
Or, we can combine both:
and then pick whichever option A has the highest .
This too will violate the independence of irrelevant alternatives and can be sensitive to how options are individuated.
Instead of summation, we could use maximums, minimums, other aggregates or voting methods.
Tournaments
Another broad class of approaches could be tournament-based ones, like a sports tournament, e.g. elimination or knockout tournaments, where competitors — here, the options — are eliminated after a certain number of losses, or group tournaments, where competitors accumulate points based on their wins and losses and are ranked accordingly.[11] There are many ways to structure tournaments, and these can be sensitive not only to which option is better and which is worse in a match between the two, but also by how much. The Wikipedia article on tournaments describes various kinds.
The approach above of calculating for each option and picking whichever has the highest is a round-robin tournament, a group tournament in which each competitor plays every other, with awarded points and awarded the negative from their match.
Podgorski (2023, pdf) develops a tournament-based approach for person-affecting population-ethical views, aiming to capture certain intuitions like the procreation asymmetry.
These too will violate the independence of irrelevant alternatives and can be sensitive to how options are individuated.
A highly permissive approach
And a much more permissive approach could be to only rule out any option that is worse than another option, and no better than any other, across all comparisons with any option as default. In other words, beats if for each option as default, and for at least one option as default.
This too will violate the independence of irrelevant alternatives, but it doesn't seem (as) sensitive to how options are individuated.
We’ll violate the independence of irrelevant alternatives
I generally expect violations of the independence of irrelevant alternatives (IIA) in the approaches described so far. In other words, how options and compare to each other can depend on whether another option is also available.
As before, if we have a sufficiently intuitive explanation for the violation, it may not bother us much or at all. I’ve only attempted to give explanations for the random option and .
We may also be able to say more about when we should and shouldn’t expect such a sufficiently intuitive explanation. For example, even if we accept some violations of IIA, we might think which option we choose should not depend on an option that is clearly dominated by another. We should rule such an option out early and then ignore it completely in the rest of our decision-making process, because it is no longer relevant once eliminated. could be clearly dominated by if . Or if stochastically dominates .
We could just identify and rule out clearly dominated options as a first step. Some decision procedures may do so as a consequence of a more general and uniform rule.
Sure vs risky options
Some of the views described above in this section can actually lend further support to riskier options than risk neutral views do. Suppose we want to compare two options:
- : one life is saved, and
- : save 1 million lives with probability 1 in a million, and do nothing otherwise.
Each option saves one life in expectation, so a risk neutral view would treat them the same.[12]
However, suppose we use to compare them.
When is taken to be the default, we have[13]
When Risky is taken to be the default, we have[14]
And
So, vastly dominates when is taken to be the default, while only slightly beats when is taken to be the default. The above approaches in this section Not privileging inaction that are sensitive to these differences, like the aggregating approaches, would suggest we go with . I'd guess (no formal proof) they would suggest no matter which increasing concave function we use, if these were the only two options. This is with no separate option for inaction, but including inaction as an option often wouldn’t make a difference.
Compared to risk neutral views, these approaches could then further favour longtermism over neartermism and invertebrate welfare over helping animals with greater probability of moral patienthood.
When making the default, the downsides of relative to it are drastically magnified. In other words, when evaluating relative , acts like insurance, and looks very risky. A sigmoidal rather than concave function could prevent this and actually give diminishing marginal returns to downsides, but it wouldn’t necessarily imply beats .
Also, in general, risky options can also be risky by having backfire risks. Such options can therefore be penalized further instead. But with the approaches above, things can go either way, or we can end up with a tie.
For example, consider : save 1 million + 100 lives with probability 1 in a million, lose 1 million - 100 extra lives with probability 1 in a million, and save 100 lives otherwise.
Taking the difference:
= save 1 million lives with probability 1 in a million, lose 1 million extra lives with probability 1 in a million, and do nothing otherwise.
And . So, if we had only these two options to consider and treated them symmetrically, we’d be indifferent between them.
- ^
Some philosophers dispute that diminishing marginal returns (concave utility functions) actually capture risk aversion or all of risk aversion, and have moved onto other ways of capturing it (Buchat, 2022, section 5, Rethink Priorities, 2023). In this piece, I will keep the presentation using diminishing marginal returns for simplicity. The arguments I make generally apply to the other accounts. I also expect that the modifications I propose later in this piece can be adapted for other accounts of risk aversion.
- ^
- ^
Or for its greater all-things-considered intuitive appeal to me, as a moral antirealist, roughly an ethical subjectivist.
- ^
My own tentative view is that diet change work increases wild (terrestrial) animal populations in expectation, and this is bad because I’m suffering-focused.
- ^
Formally, we can use their quantile functions (the inverse cumulative distribution functions) as random variables with states in the unit interval with the uniform probability over the unit interval, take statewise differences with the default option, apply our concave function to the difference in values and take the expected value.
The quantile function of a random variable as a random variable itself has the same cumulative distribution function as the original random variable, so stochastically dominates if and only if stochastically dominates .
- ^
Other possibilities include comparing to the best option, or to the worst option, or a specific outcome, but the random option seems less privileging and more agnostic.
- ^
We can think of assigning the n options the labels 1 through n randomly and without replacement, independently of any characteristics of the options themselves. Then, any fixed option has probability of having the label , for a given between 1 and . So, if our rule were to pick option , and we try to identify ahead of time, the probability that we’d succeed is .
- ^
One problem is with the individuation of options. Say an option you are considering involves pressing a button. Should we treat it as two (or more) options if you have to decide between pressing it with your right hand or left hand, even though the difference has no foreseeable effects? And there are multitudes of ways to press that button, e.g. reaching faster or slower, every precise muscle movement, and so on. The random option will depend on how exactly individuate options and their number.
Thanks to Derek Shiller for pointing this out.
In response, we can just individuate options in ways that feel most intuitive or natural. This may be fairly arbitrary.
- ^
We could have an option to flip a coin, and pick option if heads, and option if tails. In general, we can always imagine, given a set of available options, adding more options by taking probabilistic mixtures of the options already available. For one reason or another, we might not want to restrict ourselves to “pure options”, which do not involve acting randomly. It’s conceivable that we have access to a probabilistic mixture of pure options, but not every pure option of which it is a mixture. Then it’s not clear what exactly the set of available options should be, and what the random option R would be as a result.
If we took the boundary of the convex hull of the set, i.e. every probabilistic mixture of the available options, then we can’t add any more with more probabilistic mixtures, but this set is now infinite, and it’s not clear what the random option would be. However, we could still just consider all of the pure options, available directly or in probabilistic mixtures of available options, and take the uniformly random probabilistic mixture over them to be . Whether or not is actually something we could even do.
- ^
Thanks to Derek Shiller for the suggestions in this subsection.
- ^
We need not necessarily actually compare each option to every other option or even do so both ways, treating each as the default in turn. However, the spirit is really that any option could be compared to any other, or at least that we vary the “default option”.
- ^
Assume, quite implausibly in reality, that the outcome of inaction is certain.
- ^
- ^
